안녕하세요 :) 소들입니다..!
거의 한 달 전부터 저의 일정표 한 구석을 차지하던

Heap에 대해 드디어 포스팅을 해보려고 합니다...후후
사실 Python에선 Heap을 제공해주는데, Swift는 따로 제공해주지 않아서
최단 경로 알고리즘 구현 해보다가 막혀서.. ;ㅁ;.. 억지로 하게됨
그래서 급하게 포스팅을 해봅니다..!!!!
모든 포스팅은 편의 말투로 합니다~!!
1. 트리의 종류
Heap을 알기 전에 우리가 이전ㅇㅔ 공부했던 트리 개념에 덧붙여
트리 종류에 대해 먼저 간단하게 알고 갈 것임 :)
왜냐면 Heap을 구현하기 위해 알아야 함
1-1. 완전 이진 트리
왼쪽 자식 노드부터 채워지며, 마지막 레벨을 제외한 모든 자식 노드가 채워져 있는 트리

1-2. 포화 이진 트리
모든 노드가 0개 또는 2개의 자식을 가지며, 모든 Leaf 노드의 Level이 똑같은 경우의 트리

1-3. 정 이진 트리
모든 노드가 0개 혹은 2개의 자식노드를 가지는 트리(포화 이진 트리의 하위)

1-4. 편향 이진 트리
모든 노드들이 한 방향으로 편향된 트리

2. 힙(Heap)이란?
데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 "완전 이진 트리"
그러하다... 힙이라는 것은, 완전 이진 트리로 이루어져 있음!!!
근데, 최대값과 최소값을 빠르게 찾는 다는 게 무슨 말이냐면,

무슨 포도송이같네;;
뭐 힙은 이런 식으로, 최대 힙 & 최소 힙 두 가지가 있음!!!
최대 힙 : 내 자식 노드의 값은 내 값보다 작거나 같아야 한다
최소 힙 : 내 자식 노드의 값은 내 값보다 크거나 같아야 한다
위와 같은 조건이 있기 때문에 노드 그림이 저렇게 되는 것이고,
또 알아둘 것은 BST와 달리 내 왼쪽 자식, 오른쪽 자식 간의 크기는 상관 없음!!!!
최대 힙의 경우 왼쪽 자식 노드가 커도 되고, 오른쪽이 커도 됨!!
다만 내 자식 노드가 나보다 항상 작아야함(같거나)
이런 특징 때문에 최대 힙의 Root Node는 항상 최대 값이 되는 거고,
최소 힙의 Root Node는 항상 최소 값이 되는 것임!
3. 힙(Heap) 구현 전 알아보기
최대 힙과 최소 힙이 있지만, 이번엔 최대 힙에 대해 구현해볼 것임 :)
일반적으로 힙은 배열을 이용해서 구현 함!!!
BST와 달리 완전 이진 트리이기 때문에, 노드 간 index 관계를 나타낼 수 있기 때문임
무슨 말이냐면, 완전 이진 트리는 무조건 왼쪽 자식 노드부터 차례차례 채워지기 때문에,
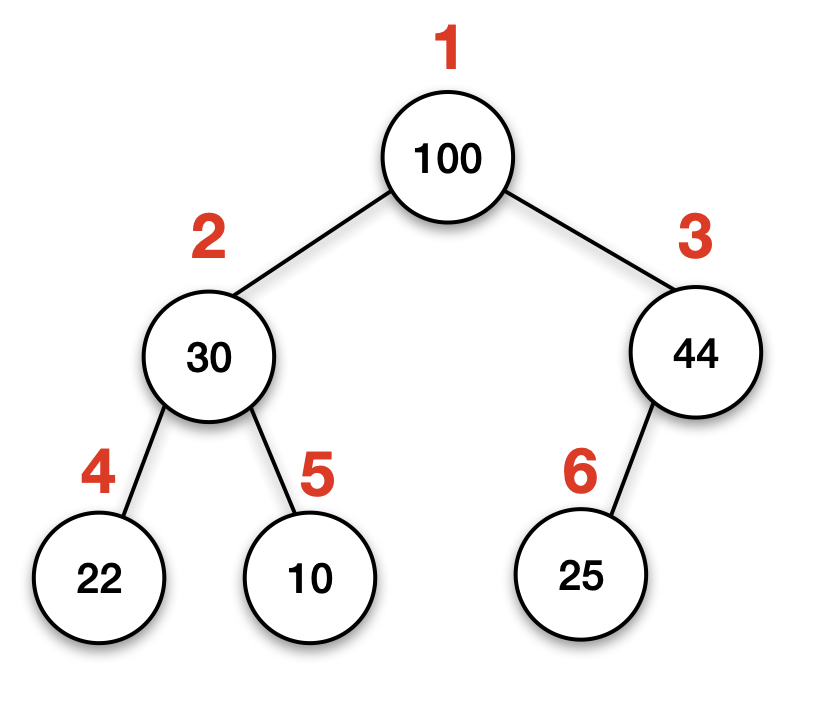
이렇게 노드가 생성되는 순서를 index로 표현할 수 있어서,
따라서 다음과 같이 부모&자식 간의 index를 서로 구할 수 있음
3-1. 부모 노드의 인덱스 번호
부모 노드의 인덱스 번호 = 자식 노드의 인덱스 번호 / 2

배열의 index는 정수형이니 어느 자식 index 번호를 나눠도 같은 값이 나옴!!
3-2. 왼쪽 자식 노드의 인덱스 번호
왼쪽 자식 노드의 인덱스 번호 = 부모 노드 인덱스 번호 * 2

3-3. 오른쪽 자식 노드의 인덱스 번호
오른쪽 자식 노드의 인덱스 번호 = (부모 노드 인덱스 번호 * 2) + 1

이런 특징이 있단 것을 염두에 둔 채로!
이제 최대 힙을 구현해 봅시다 :)
4. 힙(Heap) 구현
위에서 말했듯 힙은 배열!로 구현 할 것임 :)
근데 이때, 배열의 index는 0번부터 시작이기 때문에 헷갈릴 수 있어서
우리가 사용할 Heap의 Node의 index는 1번 index부터 시작하도록 해보겠음!!!
(0번부터 시작하면 0번노드의 자식 노드 index를 찾을 때 따로 처리해주어야 함)
4-1. 구조체를 생성하자
|
struct Heap<T: Comparable> {
var heap: Array<T> = []
init() { }
init(data: T) {
heap.append(data) // 0번 index 채우기용
heap.append(data) // 실제 Root Node 채우기
}
}
|
비교가 가능한 데이터면 모두 담게 Comparable이란 프로토콜을 채택 했고,
append를 두번 한 것은, 0번 index를 임의로 채우기 위해서임!
실제 Node의 시작은 1번 index에서부터니까!
4-2. insert(_:) : 데이터 삽입하기
먼저 데이터를 삽입하는 방법에 대해 보고 코드로 구현해볼 것임!
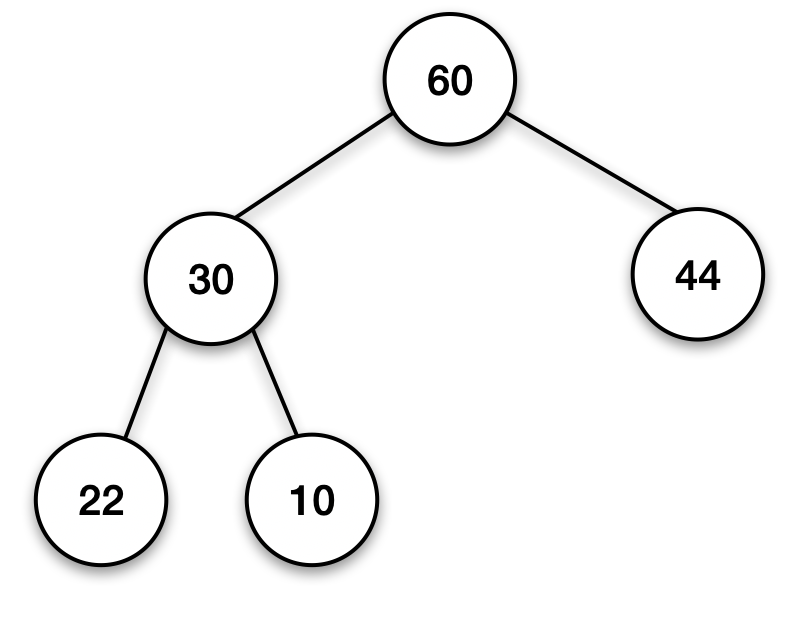
만약 이런 최대 힙에 100이란 데이터를 삽입 한다면!!!
① 완전 이진 트리 구조에 맞춰 일단 삽입한다(데이터 비교 X)
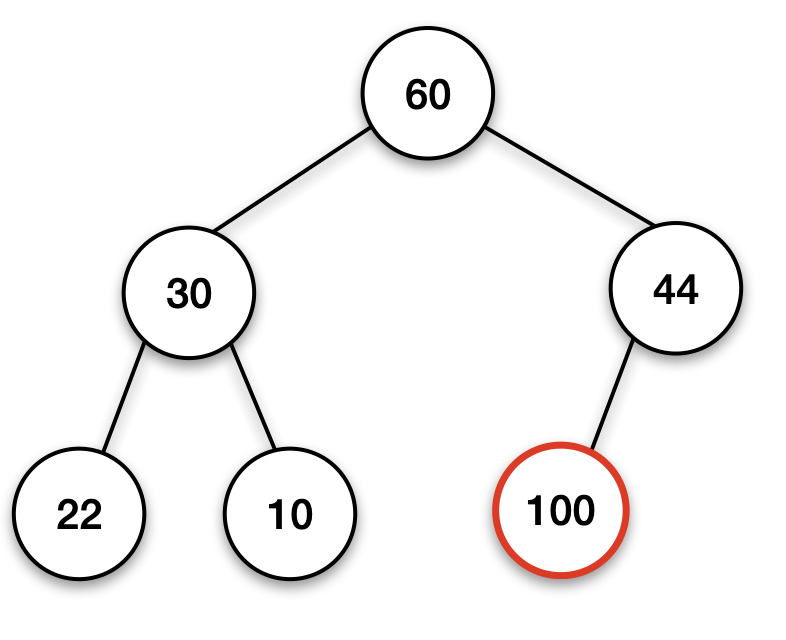
② 삽입된 데이터의 크기가 부모노드의 데이터보다 작을 때까지 swap 해준다 (반복 작업)

이렇게 부모 노드와 자기 데이터를 비교하며,
자기 데이터보다 큰 부모 노드를 찾을 때까지 swap하며 자기 자리를 찾아가는 것임
(만약 더이상 비교할 부모 노드가 없으면 rootNode라는 것)
이를 코드로 구현 하면,
|
mutating func insert(_ data: T) {
if heap.count == 0 {
heap.append(data)
heap.append(data)
return
}
heap.append(data)
func isMoveUp(_ insertIndex: Int) -> Bool {
if insertIndex <= 1 { // 루트 노드일 때
return false
}
let parentIndex: Int = insertIndex / 2
return heap[insertIndex] > heap[parentIndex] ? true : false
}
var insertIndex: Int = heap.count - 1
while isMoveUp(insertIndex) {
let parentIndex: Int = insertIndex / 2
heap.swapAt(insertIndex, parentIndex)
insertIndex = parentIndex
}
}
|
정석 방식대로 구현해봤움..!!!
이렇게 만들어 주고, 실제 테스트를 해보면..!
|
var heap = Heap.init(50)
heap.insert(100)
heap.insert(30)
heap.insert(10)
|
우리가 원하는 대로

노드가 잘 형성되어 있음!!!!! (0번 index의 값은 무시!!)
4-3. pop() : 데이터 꺼내기(삭제하기)
이번엔 힙에 저장된 데이터를 삭제하는 방법에 대해 볼 것인데,
이를 왜 꺼내기라 했냐면, 힙은 언제 쓴다? 최소값&최대값을 빠르게 찾을 때 쓴다!
따라서 최대힙에서 데이터를 꺼낸다는 것은 최대 큰 값(Root Node)를 꺼낸다는 것과 같음
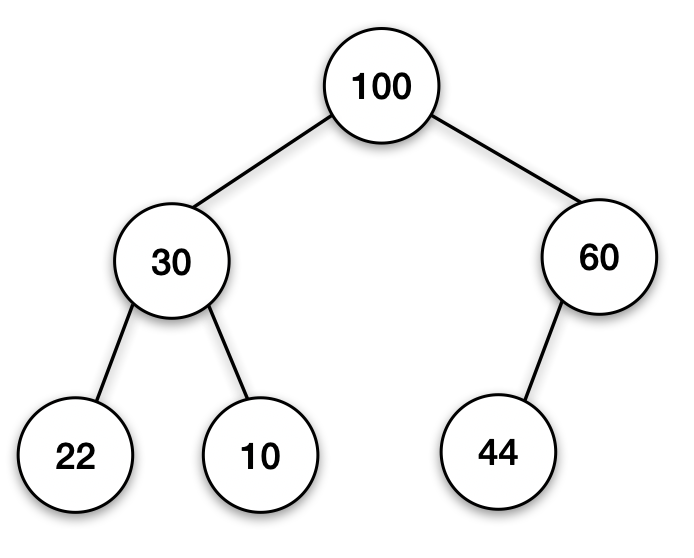
만약 이런 최대 힙에서 pop이란 메서드를 호출 한다면!!!
① 가장 큰 값인 Root Node를 삭제한다(Return 값)

② 가장 마지막에 추가된 노드(배열 마지막 요소)를 Root Node로 이동한다

③ 이동된 Root Node의 데이터가 왼쪽, 오른쪽 자식 노드의 데이터보다 클 때까지,
자식 노드 중 큰 값을 가진 노드와 swap 해준다 (반복 작업)

이렇게 얼떨결에 Root Node로 간 노드와 자식 노드들을 비교하며,
자기 데이터보다 모든 자식 노드들이 작을 때까지 swap하며 자기 자리를 찾아가는 것임
(만약 더이상 비교할 자식 노드가 없어도 끝난 것)
이를 코드로 구현 하면,
|
enum moveDownStatus { case none, left, right }
mutating func pop() -> T? {
if heap.count <= 1 { return nil }
let returnData = heap[1]
heap.swapAt(1, heap.count - 1)
heap.removeLast()
func moveDown(_ poppedIndex: Int) -> moveDownStatus {
let leftChildIndex = (poppedIndex * 2)
let rightChildIndex = leftChildIndex + 1
// case 1. 모든(왼쪽) 자식 노드가 없는 경우 (완전이진트리는 왼쪽부터 채워지므로)
if leftChildIndex >= heap.count {
return .none
}
// case 2. 왼쪽 자식 노드만 있는 경우
if rightChildIndex >= heap.count {
return heap[leftChildIndex] > heap[poppedIndex] ? .left : .none
}
// case 3. 왼쪽 & 오른쪽 자식 노드 모두 있는 경우
// case 3-1. 자식들이 자신보다 모두 작은 경우
if (heap[leftChildIndex] < heap[poppedIndex]) && (heap[rightChildIndex] < heap[poppedIndex]) {
return .none
}
// case 3-2. 자식들이 자신보다 모두 큰 경우 (왼쪽과 오른쪽 자식 중 더 큰 자식 선별)
if (heap[leftChildIndex] > heap[poppedIndex]) && (heap[rightChildIndex] > heap[poppedIndex]) {
return heap[leftChildIndex] > heap[rightChildIndex] ? .left : .right
}
// case 3-3. 왼쪽 & 오른쪽 중 한 자식만 자신보다 큰 경우
return heap[leftChildIndex] > heap[poppedIndex] ? .left : .right
}
var poppedIndex = 1
while true {
switch moveDown(poppedIndex) {
case .none:
return returnData
case .left:
let leftChildIndex = poppedIndex * 2
heap.swapAt(poppedIndex, leftChildIndex)
poppedIndex = leftChildIndex
case .right:
let rightChildIndex = (poppedIndex * 2) + 1
heap.swapAt(poppedIndex, rightChildIndex)
poppedIndex = rightChildIndex
}
}
}
|
일단 설명(주석)이 들어가느라 코드가 좀 길어졌고.. (주석 빼고 보면 별로 안 긺)
처음 짜보는 거라 약간 너무 난잡한데 코드가..........;;;;;;;;
지금은 알고리즘 병아리이니.. 나중에 더 효율적인 코드를 짠다면 수정 하겠음!!
(혹시 코드 문제점이나 피드백 있을 시 댓글 꼭 주세요ㅠ.ㅠ)
remove 과정또한 테스트로 확인해 보면..!!!
|
var heap = Heap.init(30)
heap.insert(20)
heap.insert(18)
heap.insert(9)
heap.insert(6)
heap.insert(50)
print(heap)
print("pop data == \(heap.pop()!)")
print(heap)
|
우리가 원하는 대로

가장 큰 값인 50이 return되고!
나머지 데이터가 최대 힙으로 다시 정렬됨!!!!!!! 오예
+ 전체 코드는 끝나기 전에 깃허브 주소로 올려둘게요 :)
5. 힙의 시간 복잡도
자, 마지막으로 힙의 시간 복잡도를 알아볼 것임!!!
힙의 시간 복잡도는
𝑂(𝑙𝑜𝑔𝑛)
한 번 실행 시마다 50%의 실행을 제거할 수도 있단 의미!
따라서, 만약 배열에 데이터를 넣고 최대&최소를 찾으려면 𝑂(𝑛)이 걸리지만,
힙에 넣을 경우 𝑂(𝑙𝑜𝑔𝑛) 으로 빠르게 찾을 수 있어서,
우선순위 큐 같이 최댓값 & 최소값을 빠르게 찾아야 되는 알고리즘이나 자료구조에 활용됨 :)
.
.
.
귀찮아서 미루다 미루다 하는 힙 포스팅....ㅎ
처음 짠 코드라 효율성 없고 버그가 있을 수 있으니 혹시 발견하신다면 꼭 댓글 주세요!!
전체 코드는 아래 주소에서 확인하실 수 있습니다 :)
- Swift 최대힙, 최소힙 코드 -
github.com/sossam/SwiftHeap/tree/main/Heap
sossam/SwiftHeap
Contribute to sossam/SwiftHeap development by creating an account on GitHub.
github.com
'Algorithm > 알고리즘' 카테고리의 다른 글
| Swift) 최소 신장 트리 :: 크루스칼 알고리즘(Kruskal’s algorithm) 구현 해보기 (0) | 2021.02.02 |
|---|---|
| Swift) 최단 경로 :: 다익스트라(Dijkstra) 구현 해보기 (5) | 2021.01.27 |
| Swift) 탐욕법 (Greedy Algorithm) + 프로그래머스 체육복 풀이 (4) | 2021.01.25 |
| Swift) 깊이 우선 탐색(DFS) 구현 해보기 (10) | 2021.01.20 |
| Swift) 너비 우선 탐색(BFS) 구현 해보기 (3) | 2021.01.20 |



