안녕하세요 :) 소들입니다!!!
오늘은 저번 포스팅에 이어 이진탐색트리에 대해 끝맺음을 해보려고 해요!!!
저번에 insert, search 하는 방법을 봤었다면,
이번 포스팅에선 노드를 remove하는 방법에 대해 알아볼 것입니다 :)
먼저 얘기하자면 난이도가 꽤 있어요!!!
remove 하는 방식에도 여러 가지 case가 존재하기 때문에 복잡하지만,
하나하나씩 차근차근 봅시다 :)
아, 그리고 재귀함수를 쓴다면 훨씬 간단하게 짤 수 있지만..!
그렇기엔 초보자분들이 이해하기 힘들 거라 생각해서 정석 코드대로 짜보려고 합니다..!
참고로 Swift로 된 코드가 거의 없어서,
제가 짠 코드가 절대 절대 정답도 아니고!!
혹시 개선 사항, 피드백, 궁금점은 언제나 댓글 주시면 감사하겠습니다 😇
음.. 이번 포스팅은 1편과 이어져서 봐야하기 때문에..!
1편에 이어서 쓰겠습니다..! 만약 1편 안 봤다면 보고 오세영
모든 포스팅은 편의 말투로 합니다~!!
③ remove(from:) : 데이터 삭제하기
정상적으로 삭제가 됐는지 여부를 리턴하는 함수를 만들어보려는데..
이진 탐색 트리에서 삭제는 매우매우 복잡함...!
따라서 다음과 같이 3가지 경우로 나누어서 보는게 좋음
(1) Child Node가 하나도 없는 Leaf Node 삭제
Leaf Node는 다음과 같이
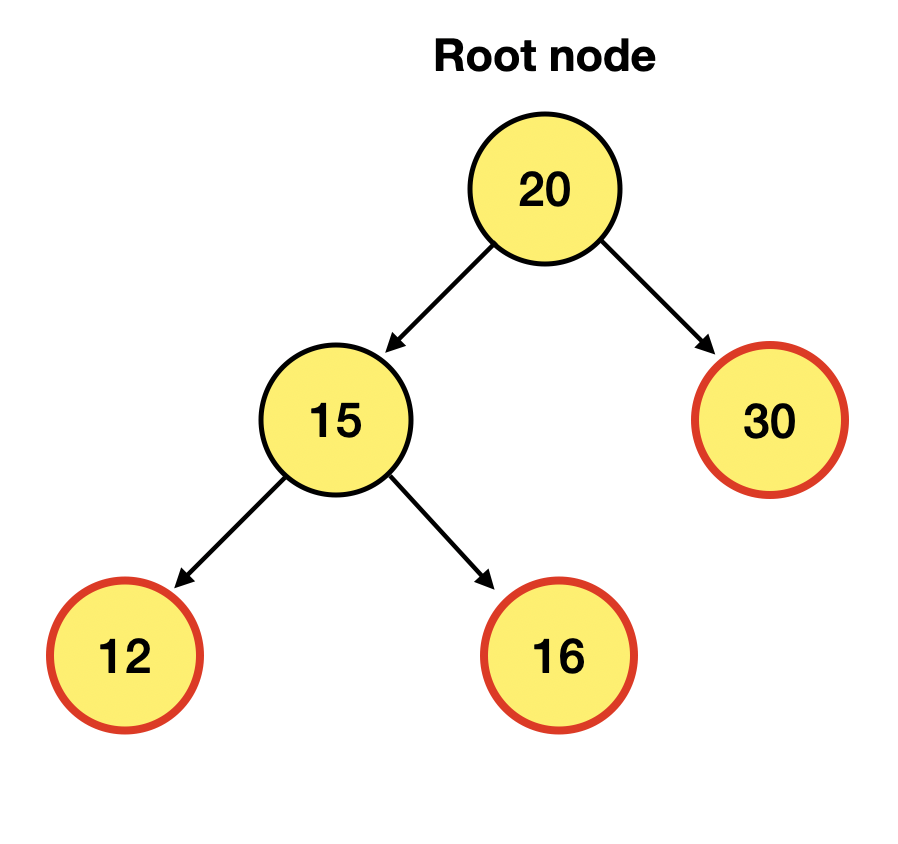
Child Node를 가지고 있지 않는 노드를 말한댔음!
따라서 위에선 12, 16, 30이 Leaf Node에 해당함!
이렇게 자식이 하나도 없는 노드를 삭제하는 것은 매우매우 간단함
삭제할 Node의 Parent Node가 삭제할 Node를 가리키지 않게 한다
이러면 끝임
만약 내가 위 그림에서 30이란 노드를 삭제하고 싶으면
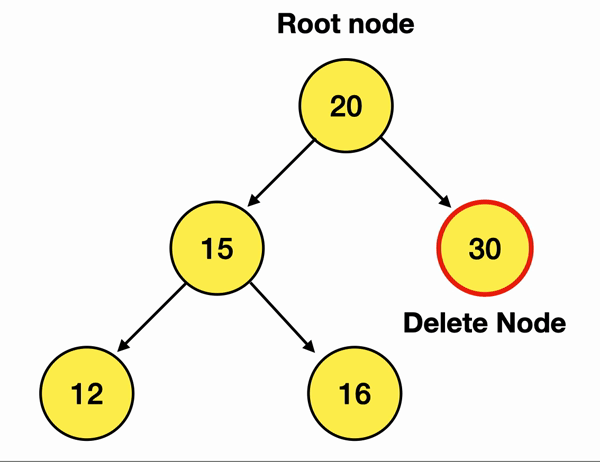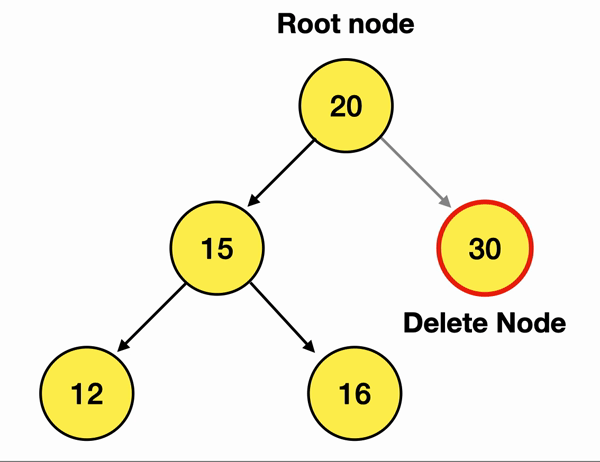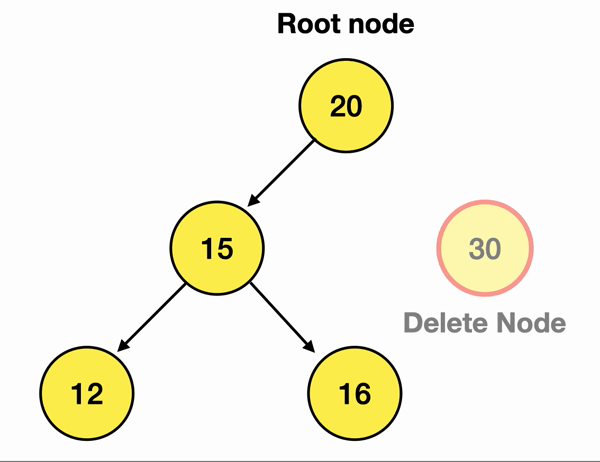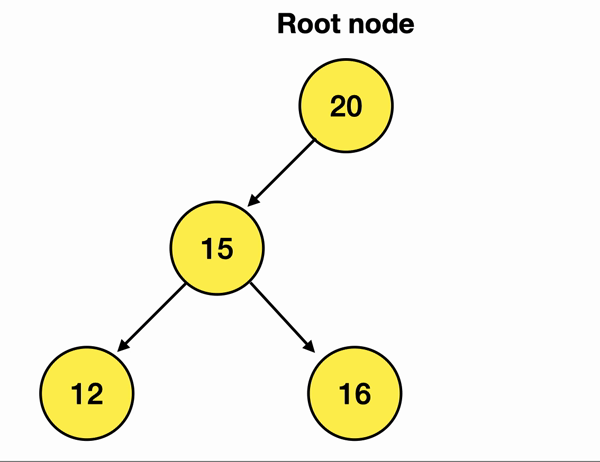
Delete Node인 30의 Parent Node인 20의 branch를 끊어주면 됨!
(연결을 끊어주는 것만으로 삭제가 가능한 것은
Node가 Class로 구현되어 Reference Count가 0이되면 ARC에 의해 자동으로 해제되기 때문 :))
자, 여기서 중요한거!!!
우리는 노드를 삭제하기 위해선 insert와 마찬가지로,
가장 먼저, 삭제할 노드를 탐색하는 작업이 필요함..!
근데, 위에서 봤듯이 근본적으로 삭제를 하는 것은
Parent Node의 branch(left 혹은 right)를 끊어주는 것(nil을 할당하는 것)이기 때문에,
- 삭제할 Node
- 삭제할 Node의 Parent Node
총 두 가지의 노드를 탐색해서 가지고 있어야함!!!
이것은 Leaf 노드 삭제뿐 아니라 삭제 작업의 기본임!!! 코드로 봐보자 :)
|
func remove(from data: T) -> Bool {
guard let root = self.root else { return false }
var parentNode = root
var currentNode: Node? = root
//삭제할 노드 탐색
while let node = currentNode {
if node.data == data { break }
if node.data > data {
currentNode = node.left
} else {
currentNode = node.right
}
parentNode = node
}
guard let deleteNode = currentNode else { //탐색 실패
return false
}
}
|
위 코드까지가 삭제할 노드와, 삭제할 노드의 Parent 노드를 탐색하는 작업임!
만약 찾기를 실패한 경우, 찾는 값 엄서용! 하고 false를 리턴해주는 것임
여기까진 remove의 공통 작업인데..
처음에 parentNode와 currentNode에 같이 옵셔널 바인딩 된 root를 넣는데,
왜 currentNode는 Type Annotation을 써서 굳이 Optional Type으로 선언하냐면,
코드를 보면 알겠지만,
parentNode는 nil이 할당될 일이 없음. 옵셔널 바인딩 된 값만 넣기 때문에!
하지만 currentNode는 탐색이 실패할 경우 nil이 할당되기 때문에 Optional Type이어야 함!!!
따라서 저렇게 해준 것인데
흠................아직은 배움이 짧아 이렇게 밖에 생각이 안 나네염 .......
뭔가 더 개선된 코드가 있다면 알려주세영:) 저도 알게 되면 추가하겠음!!! 🌝
이제부터 Leaf Node를 삭제할 때는 다음과 같이 짜면 될듯함
|
// 1. 자식이 없는 노드 삭제(Leaf Node)
if deleteNode.left == nil && deleteNode.right == nil {
if parentNode.data > data {
parentNode.left = nil
} else {
parentNode.right = nil
}
return true
}
|
쉽죠 :))))) 실제 결과로 확인해볼까염?
|
let BST = BinarySearchTree<Int>()
BST.insert(20)
BST.insert(15)
BST.insert(30)
BST.insert(12)
BST.insert(16)
BST.insert(35)
BST.insert(37)
BST.remove(from: 37)
|
이렇게 트리를 insert하고 Leaf Node인 37을 삭제하고 다이어그램으로 확인해보면
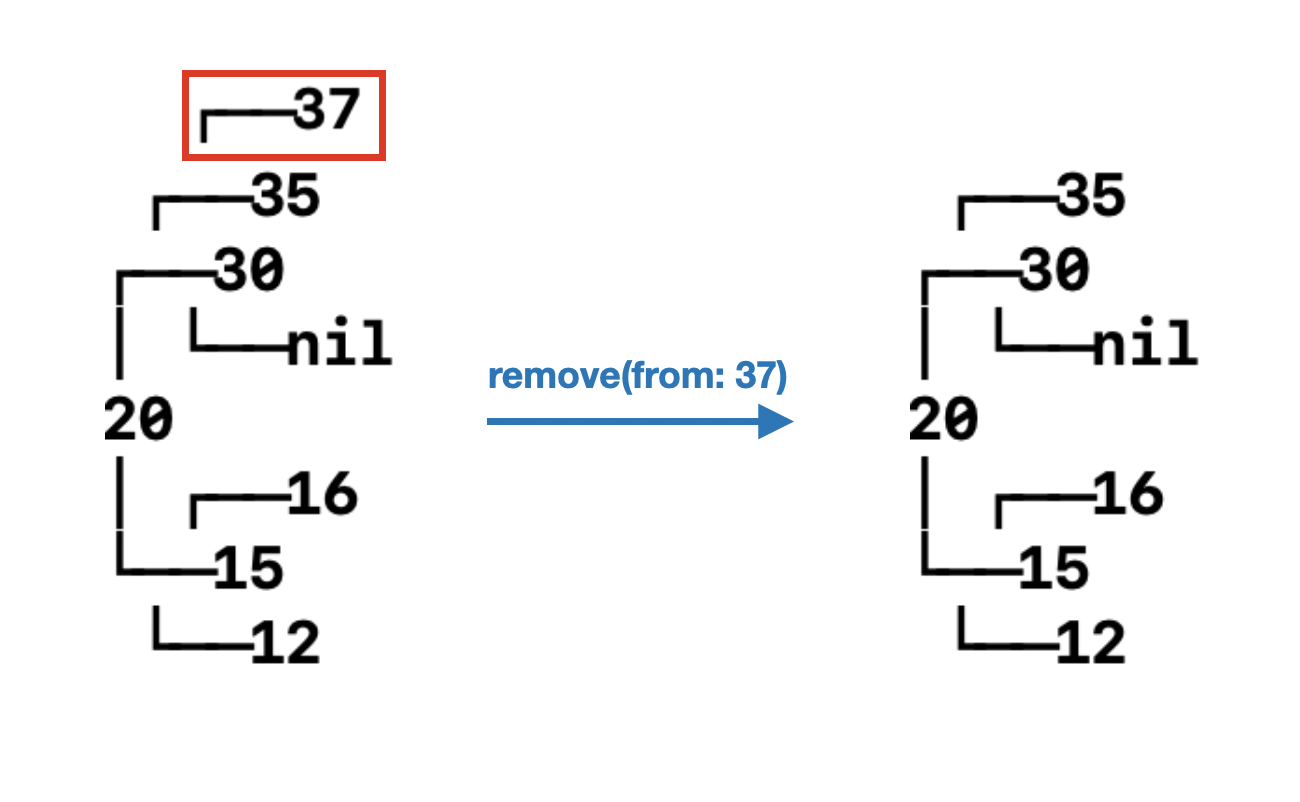
이렇게 37이 삭제된 것을 확인할 수 있다~
Leaf 노드일 땐 이렇게나 쉬움^^
(2) Child Node가 하나만 있는 Node 삭제
자, Child Node가 하나 있는 노드는
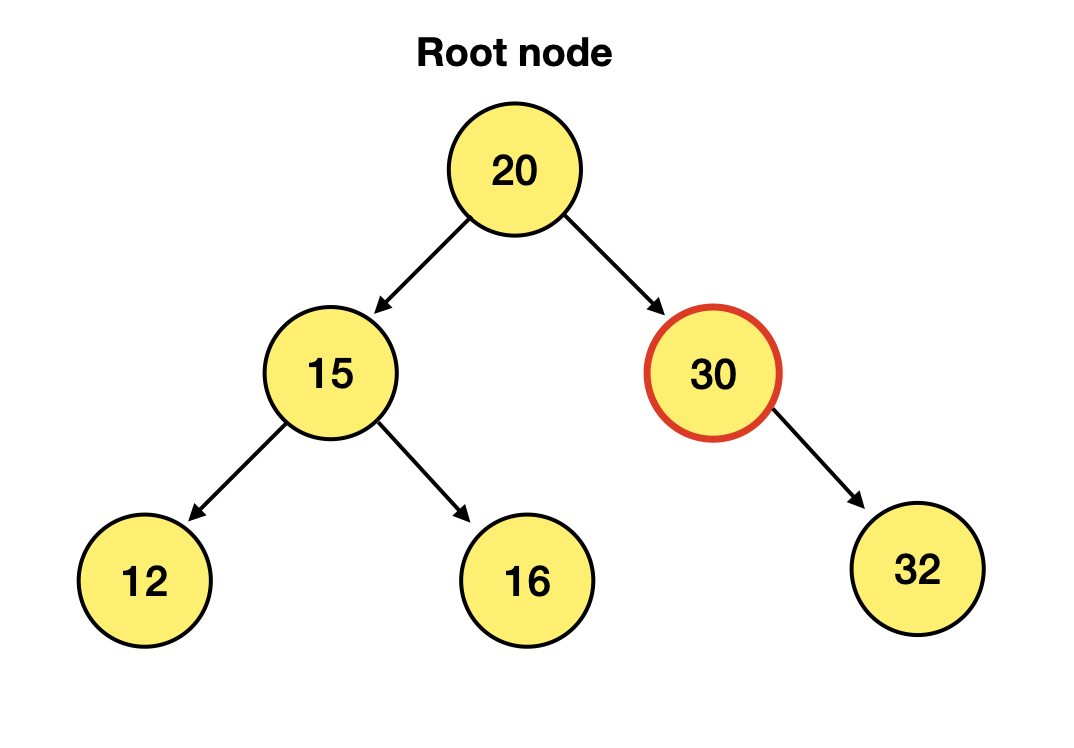
위에서 30이란 노드에 해당하잖음?근데 이것은 어떻게 삭제할까?
어렵지 않음 이또한 매우 간단쓰
삭제할 노드의 Parent Node가 삭제할 Node의 Child Node를 가리키게 한다
이러면 끝임
만약 내가 위 그림에서 30이란 노드를 삭제하고 싶으면
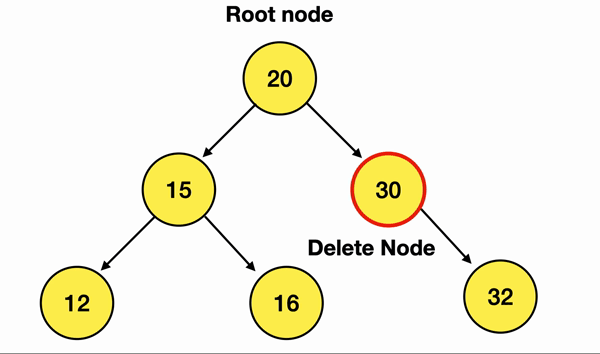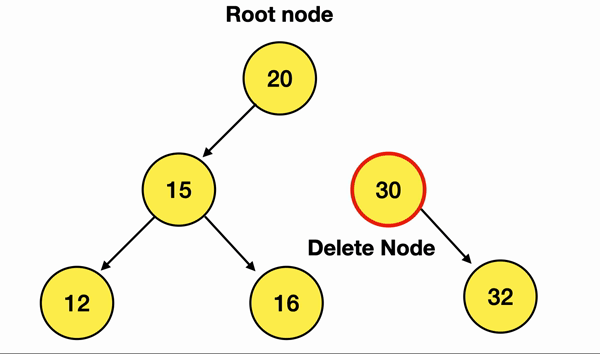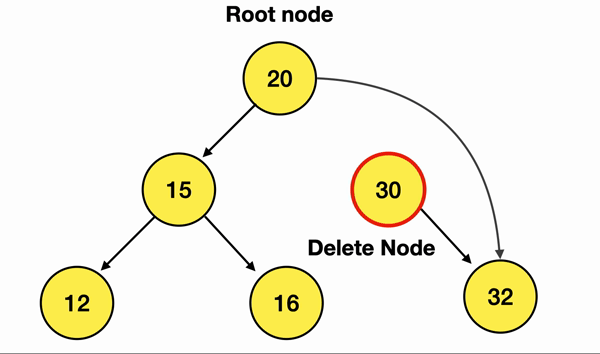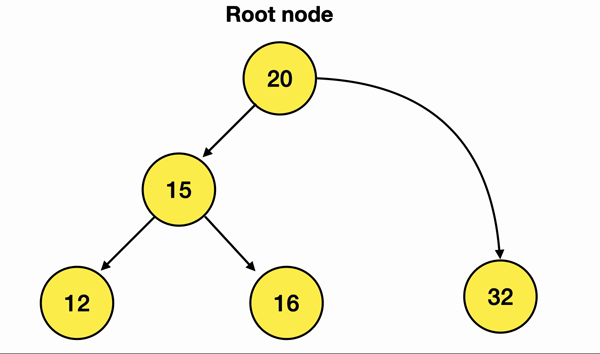
이렇게 해주면 된다는 말임 :)
늘 말했듯 참조가 끊긴 Delete Node는 ARC에 의해 알아서 해제됨 XD
코드로 보면 다음과 같음!!!!
|
// 2. 자식이 1개 있는 노드 삭제
if (deleteNode.left != nil) && (deleteNode.right == nil) { // 왼쪽 자식 노드가 존재할 경우
if parentNode.data > data {
parentNode.left = deleteNode.left
} else {
parentNode.right = deleteNode.left
}
return true
}
if (deleteNode.left == nil) && (deleteNode.right != nil) { // 오른쪽 자식 노드가 존재할 경우
if parentNode.data > data {
parentNode.left = deleteNode.right
} else {
parentNode.right = deleteNode.right
}
return true
}
|
차근차근 짜보면 어렵지 않음!!!!!! 실제 테스트 해보자 :)
|
let BST = BinarySearchTree<Int>()
BST.insert(20)
BST.insert(15)
BST.insert(30)
BST.insert(12)
BST.insert(16)
BST.insert(32)
BST.remove(from: 30)
|
오른쪽 자식 노드 하나를 가진 30을 삭제하는 것을 다이어그램으로 확인해보면,
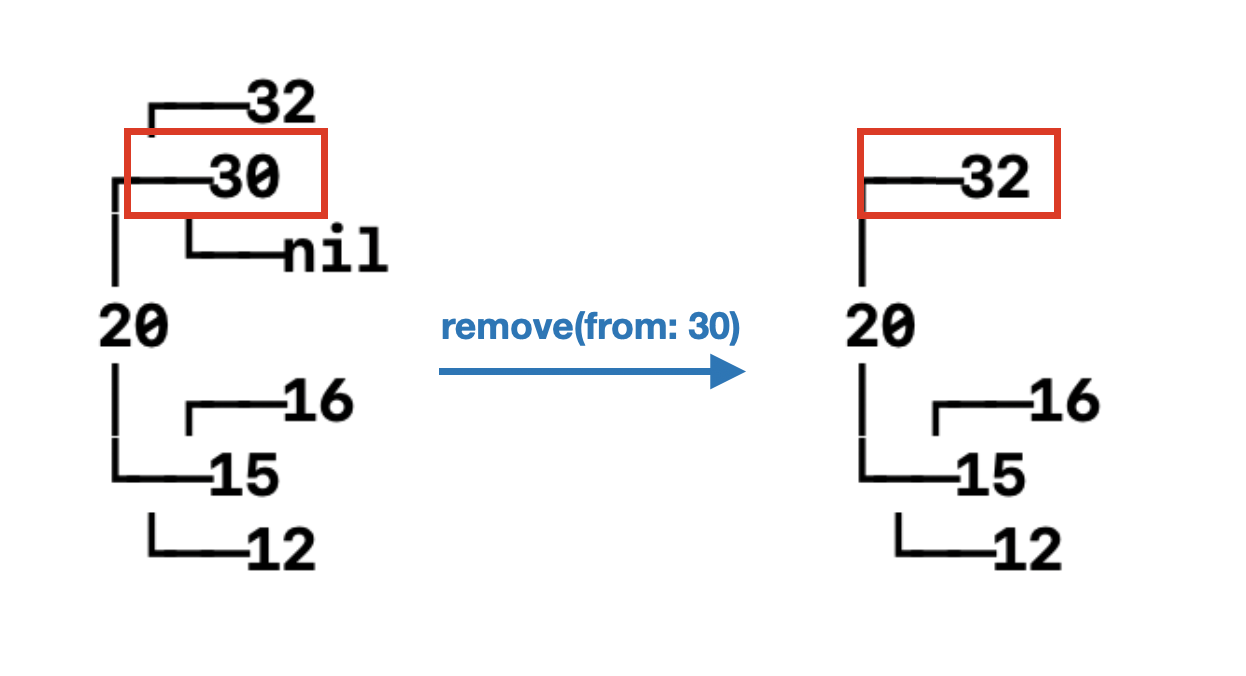
30의 자식노드인 32가 30의 부모노드인 20하고 연결되고,
30은 삭제된 것을 볼 수 있음 :))))
(3) Child Node가 두 개 있는 Node 삭제
OTL.. 이부분이 조금 어려움!!!! 헷갈릴 수 있으니 개념부터 차근차근 공부해봅시다 :)
자, 다음과 같은 이진 탐색 트리가 있을 때, 자식 노드가 두 개 있는 노드는
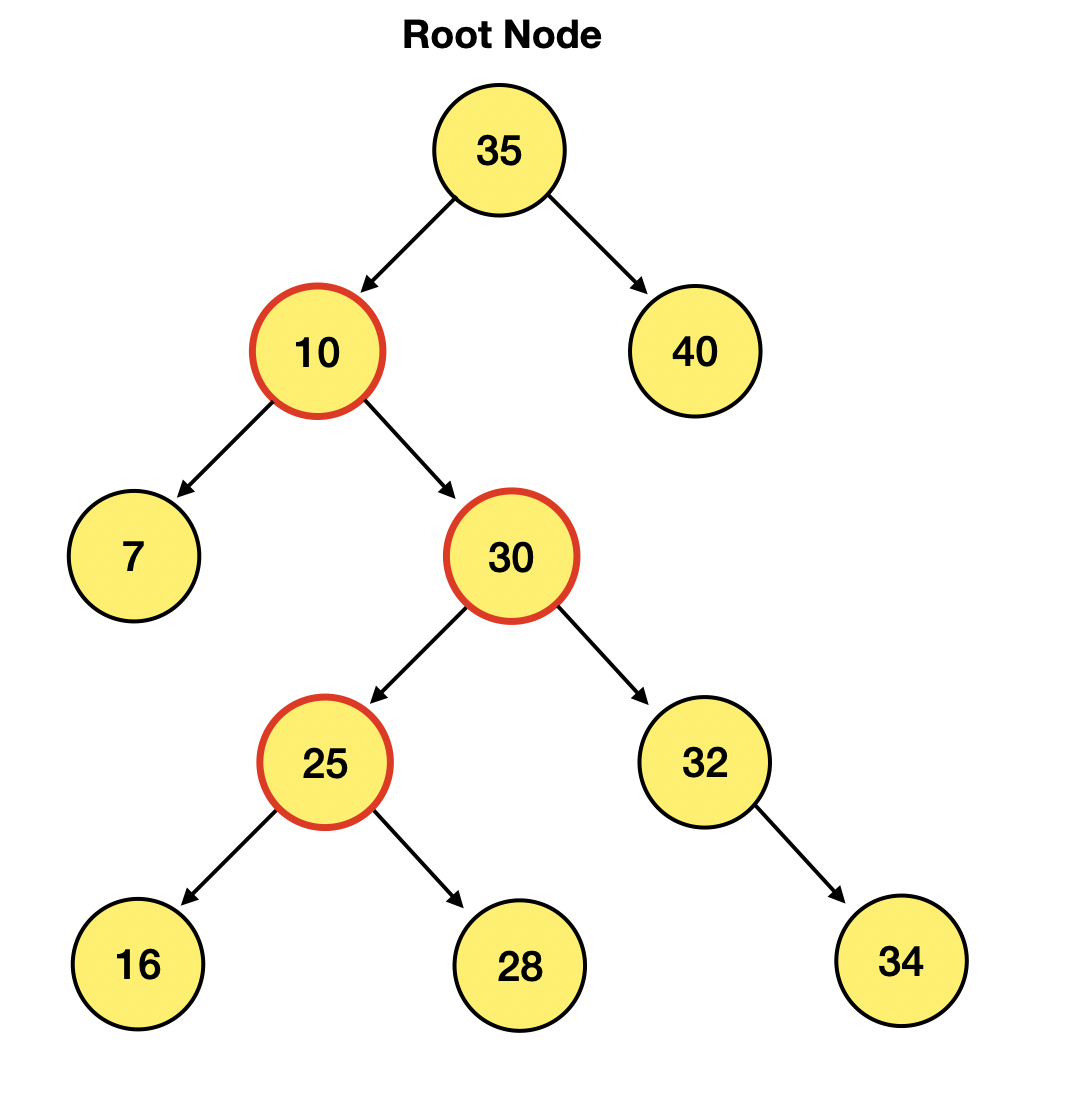
루트 노드를 제외하고 10, 30, 25 총 세개의 노드에 해당함!!
이중에서 10을 삭제하고 싶다!!!!!!! 하면 방법이 무려 2가지 방법이 있음
1️⃣ 삭제할 노드의 "오른쪽" 자식 노드 중,
가장 "작은" 값을 찾아 삭제할 노드의 부모 노드가 가리키게 한다
자.. 근데 이렇게 나뉜 경우에도 또 두 가지 케이스가 있음.... ㅎ 하 케이스 🐶많다 정말..
가장 작은 값을 가진 노드에 오른쪽 자식 노드가 존재할 수도 있기 때문인데.. 그림으로 봅시다!
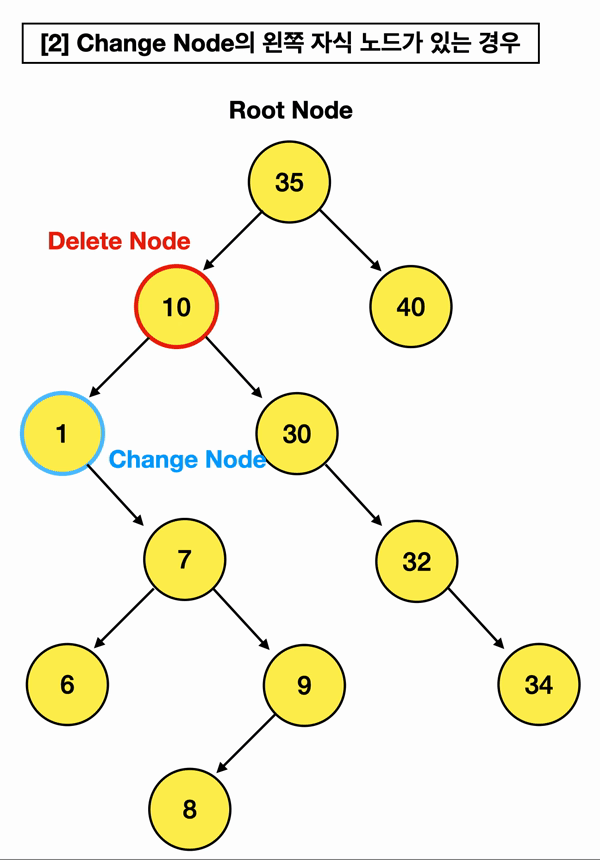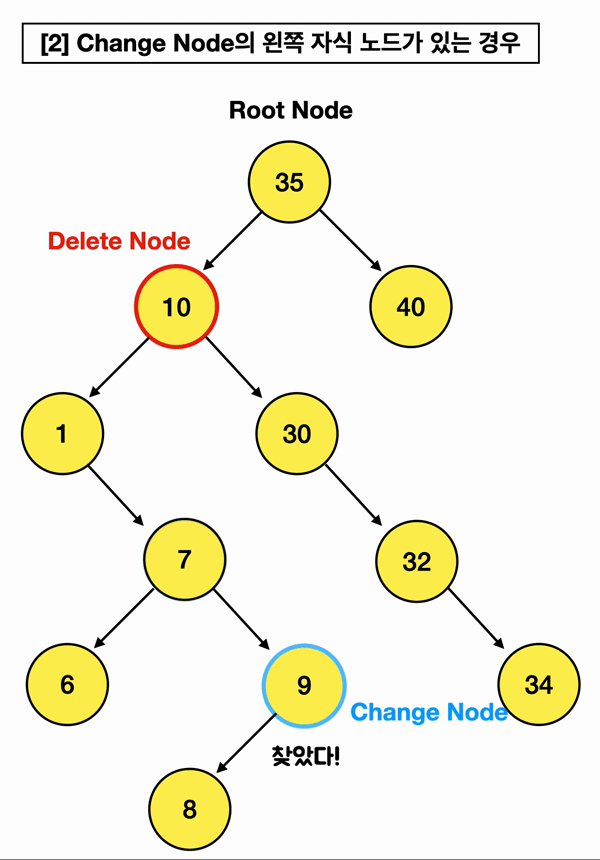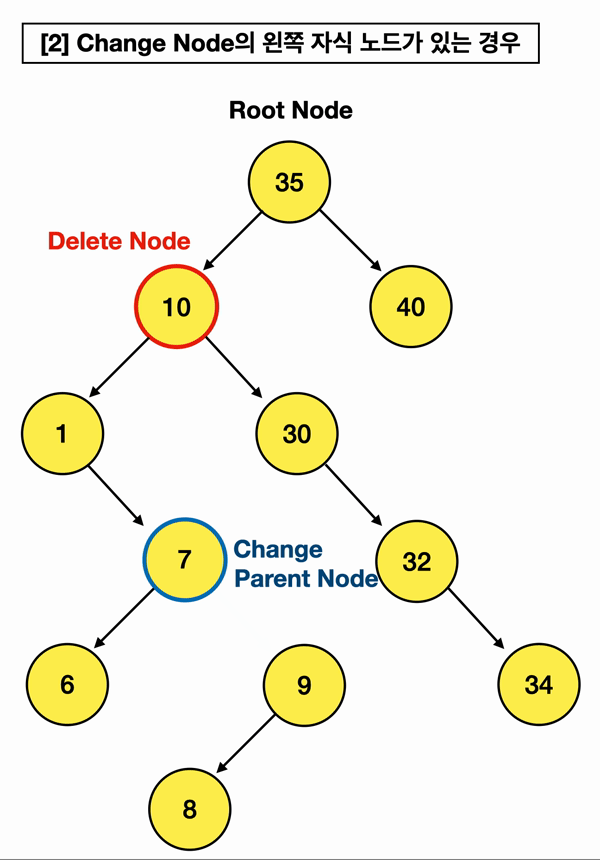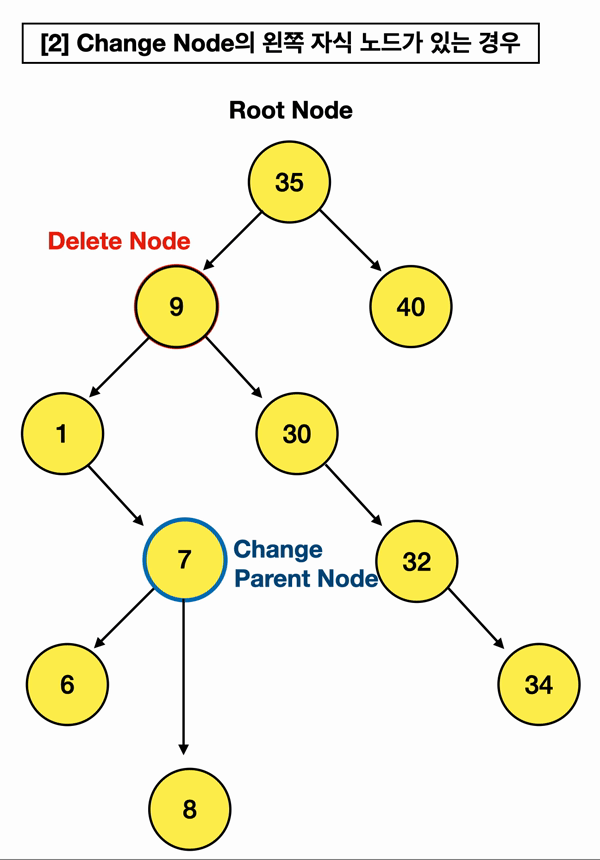
삭제할 노드 오른쪽 자식 노드 중 가장 작은 값을 가진 노드를 Change Node라고 하겠음
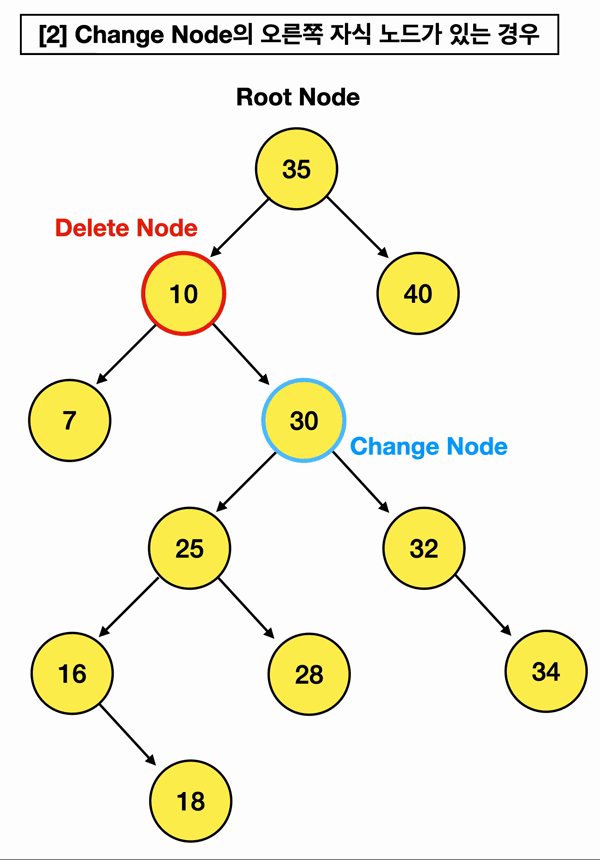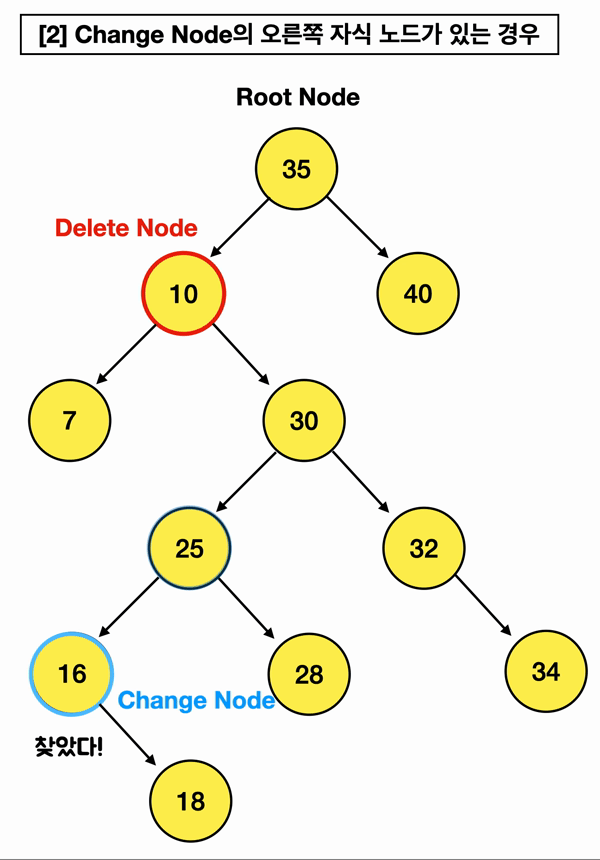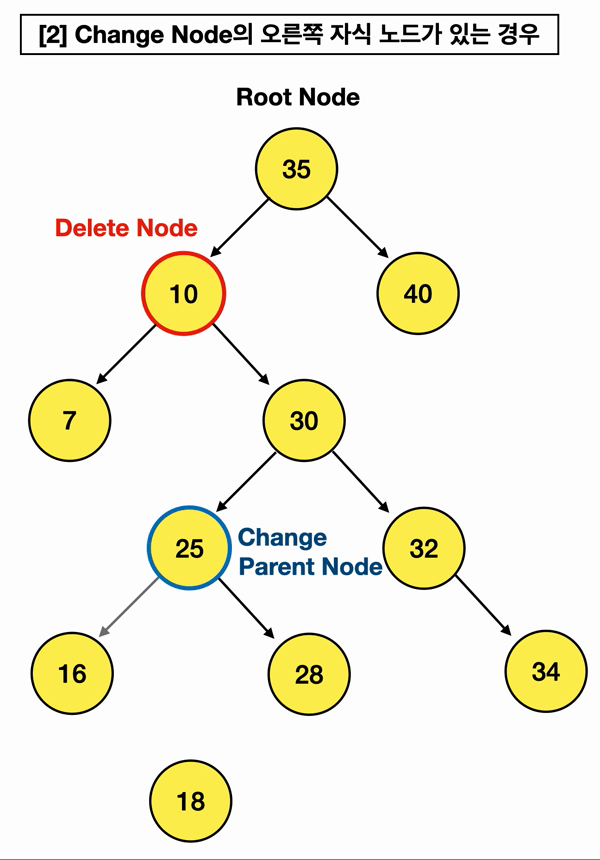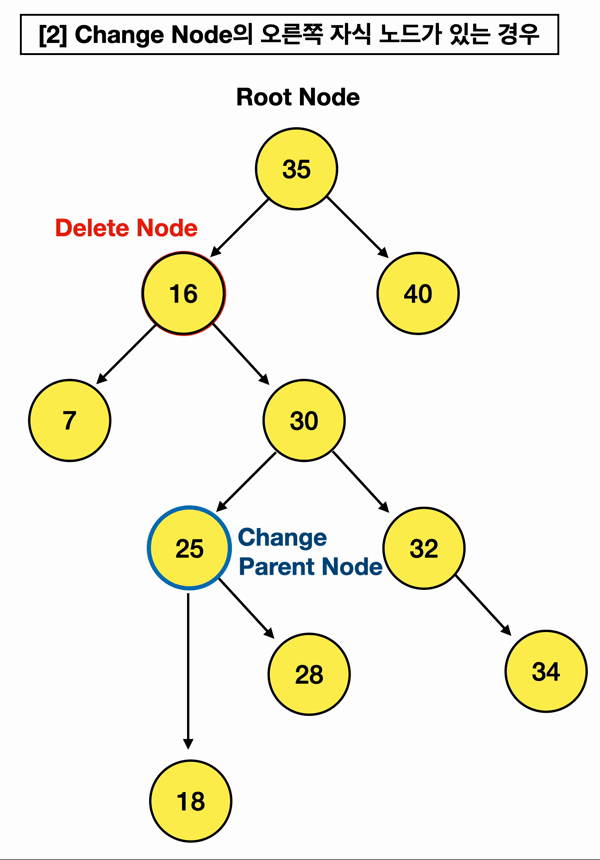
ㅎ..... 키노트로 짤만들기 빡세다
최대한 이해가 가게끔 만들었는데.. 어쨌거나 동작 방식은 위와 같음!!!
내 삭제할 노드(10)의 오른쪽 자식노드(30) 중에
가장 작은 값, 즉 Change Node을 찾아서 삭제할 노드의 부모 노드(35)가 가리키게끔 하는 것임!!!
*주의*
그림에선 이해하기 편하라고 마지막에 Change Node가 Delete Node 자리로 이동했지만,
실제 코드에선 Delete Node의 Parent Node(10)의 branch를 Change Node(16)로 바꿔주어야 하고,
때문에 Delete Node의 left, right를 Change Node의 left, right로 이식수술 해줘야 함
그리고 한 가지 알 수 있는 사실은, 이진 탐색 트리는 이미 삽입부터 정렬되어 있는 구조기 때문에!!!
오른쪽 자식의 가장 작은 값은, 오른쪽 자식 노드 중 가장 왼쪽 끝에 위치한 자식 노드라는 것을 알 수 있음!!
(걍 쉽게말해 삭제할 오른쪽 자식 노드에서 왼쪽 왼쪽 왼쪽으로만 쭉 가면 된단 말임)
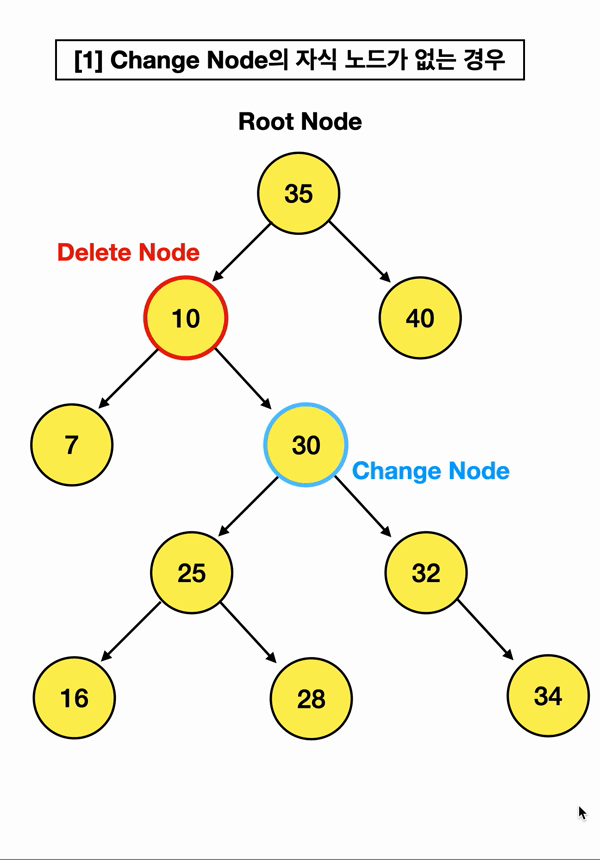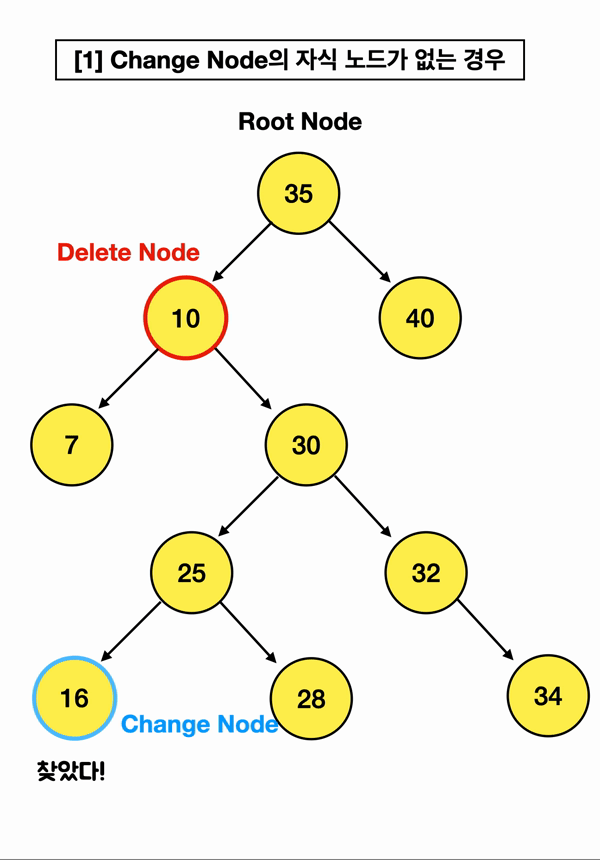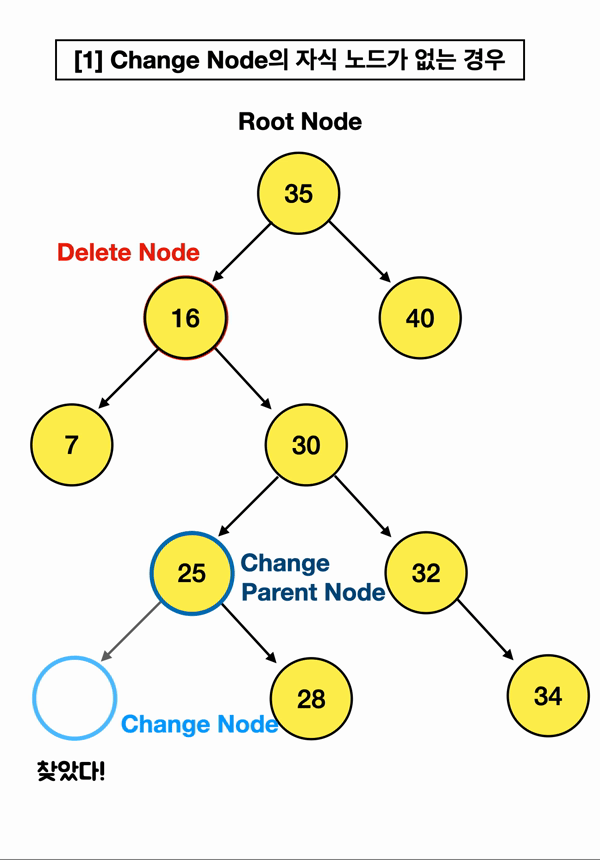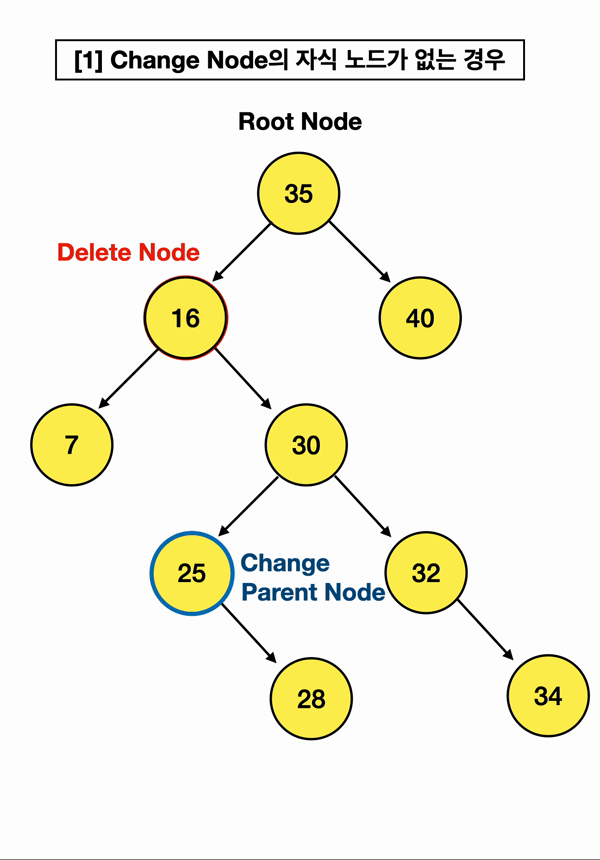
근데 만약 Change Node를 찾았는데 Change Node가 오른쪽 자식 노드(18)를 가지고 있다?
[2]번 경우가 그런데, 이럴 땐 이 오른쪽 자식 노드(18)를,
Change Node의 부모인 Change Parent Node의 "왼쪽" branch로 연결해주는 것임
(Change Node는 왼쪽 자식 노드를 가질 수는 없음.
왜냐? 왼쪽 자식 노드는 Change Node보다 작은 값이어야 할테니까,
그럼 Change Node가 가장 작은 값이 아니란 말이니까)
쨌든, 우리가 코드로 찾아야 할 것은 가장 먼저
Change Node를 찾아야 하고, Change Node의 Parent Node도 찾아서 알고 있어야 함!
만약 이해가 안된다면 그림으로 보면서 찬찬히 이해하시길 :)
2️⃣ 삭제할 노드의 "왼쪽" 자식 중,
가장 "큰" 값을 찾아 삭제할 노드의 부모 노드가 가리키게 한다
이또한 두 가지 경우가 있고,
위와 다른 점은 "왼쪽" 자식부터 시작해서, 가장 "큰 값"을 찾는다는 점임!
따라서 Change Node가 삭제할 노드의 왼쪽부터 시작함
그림만 투척하고 사라지겠음
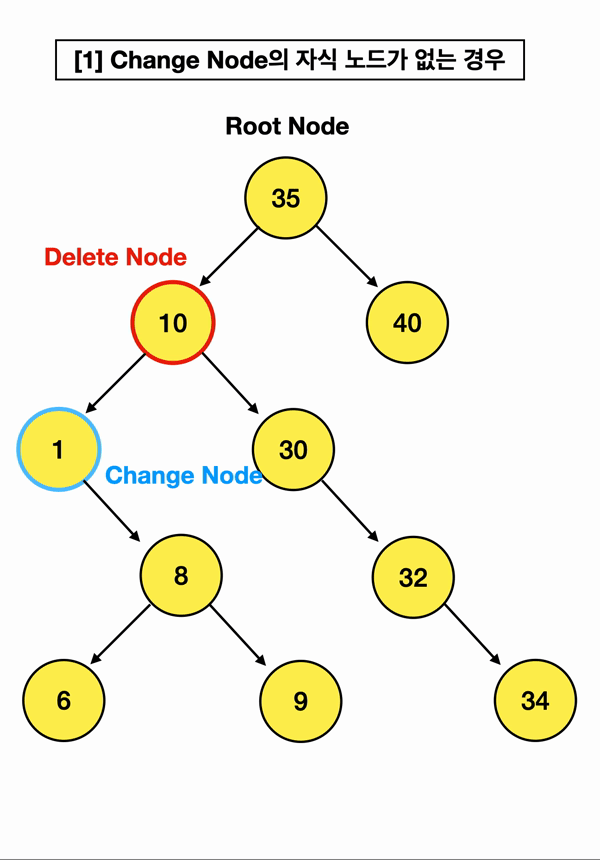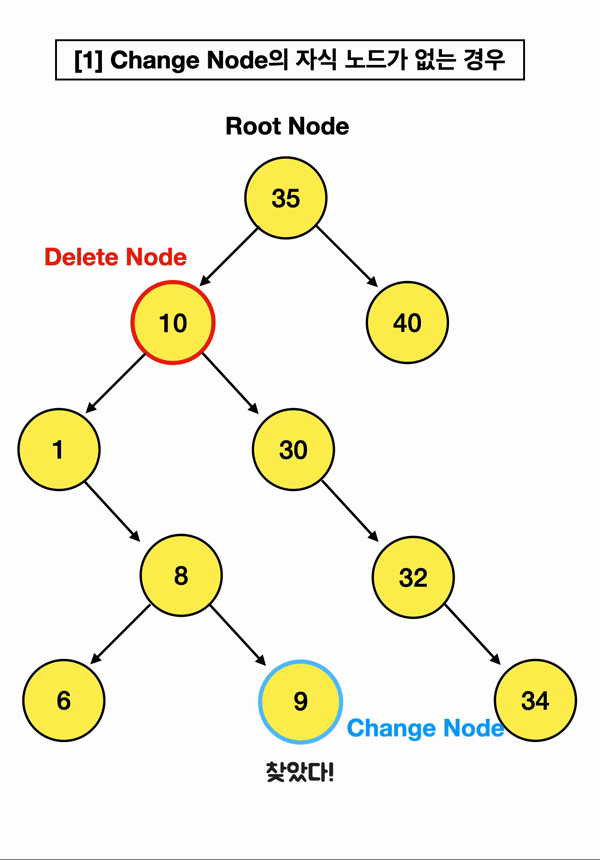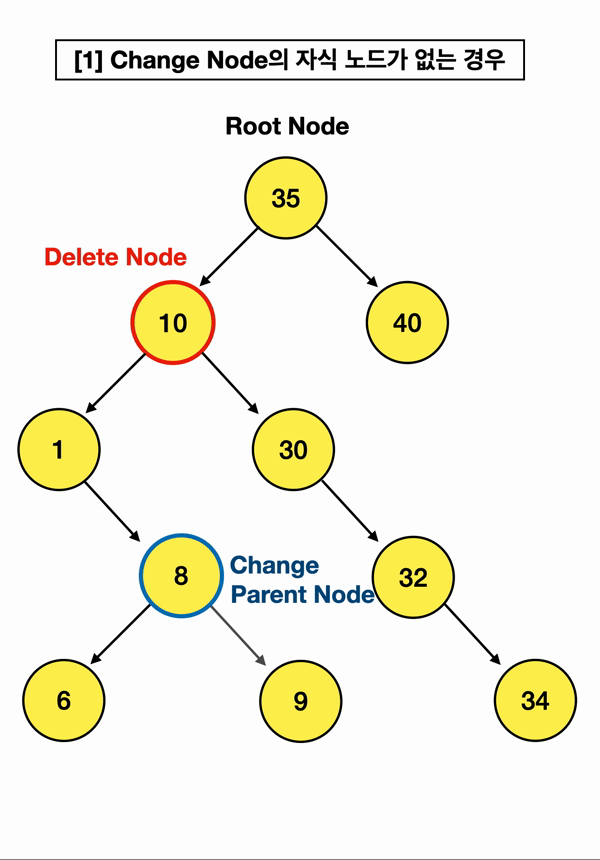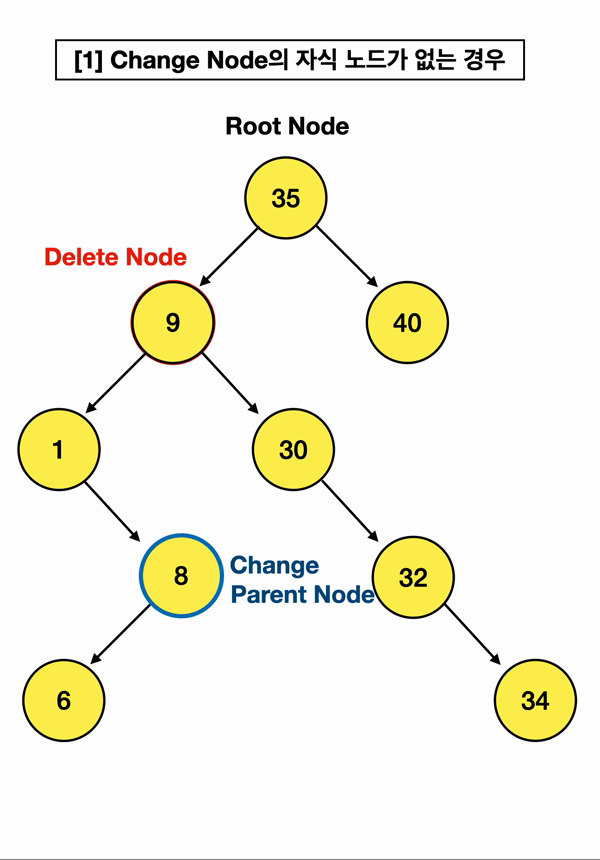
이또한 마찬가지로 한 가지 알 수 있는 사실은, 앞서 말했듯 이미 삽입부터 정렬되어 있는 구조기 때문에!!!
왼쪽 자식의 가장 큰 값은, 왼쪽 자식 노드 중 가장 오른쪽 끝에 위치한 자식 노드라는 것을 알 수 있음!!
(걍 쉽게말해 삭제할 왼쪽 자식 Node에서 오른쪽 오른쪽 오른쪽으로만 쭉 가면 된단 말임)
.
.
와 정말 길고 길었다 ^^..;;;;
위에서 두 가지 방법을 설명 했지만
나는 1️⃣번 방법으로 한번 코드로 구현을 해보겠음 :)
|
// 3. 자식이 2개 있는 노드 삭제
guard let rightNode = deleteNode.right else { return false }
var changeNode = rightNode
var changeParentNode = rightNode
while let nextNode = changeNode.left {
changeParentNode = changeNode
changeNode = nextNode
}
if let changeChildNode = changeNode.right {
changeParentNode.left = changeChildNode
} else {
changeParentNode.left = nil
}
if parentNode.data > data {
parentNode.left = changeNode
} else {
parentNode.right = changeNode
}
// Delete Node의 왼쪽, 오른쪽 자식을 changeNode에게 이식
changeNode.left = deleteNode.left
changeNode.right = deleteNode.right
return true |
이렇게 짜주면 되겠다!! :)
정말 정석 정석 정석방식 그대로 짜봤음...
옵셔널 바인딩이 여전히 까다롭긴 하지만, 문제는 없고 테스트를 해봅시다~~
|
let BST = BinarySearchTree<Int>()
BST.insert(35)
BST.insert(10)
BST.insert(40)
BST.insert(7)
BST.insert(30)
BST.insert(25)
BST.insert(32)
BST.insert(16)
BST.insert(28)
BST.insert(34)
BST.insert(18)
print(BST.remove(from: 10))
|
위 예제처럼 노드를 insert 하고,
두 개의 자식을 가지는 10번 노드를 삭제한 후 다이어그램으로 보면
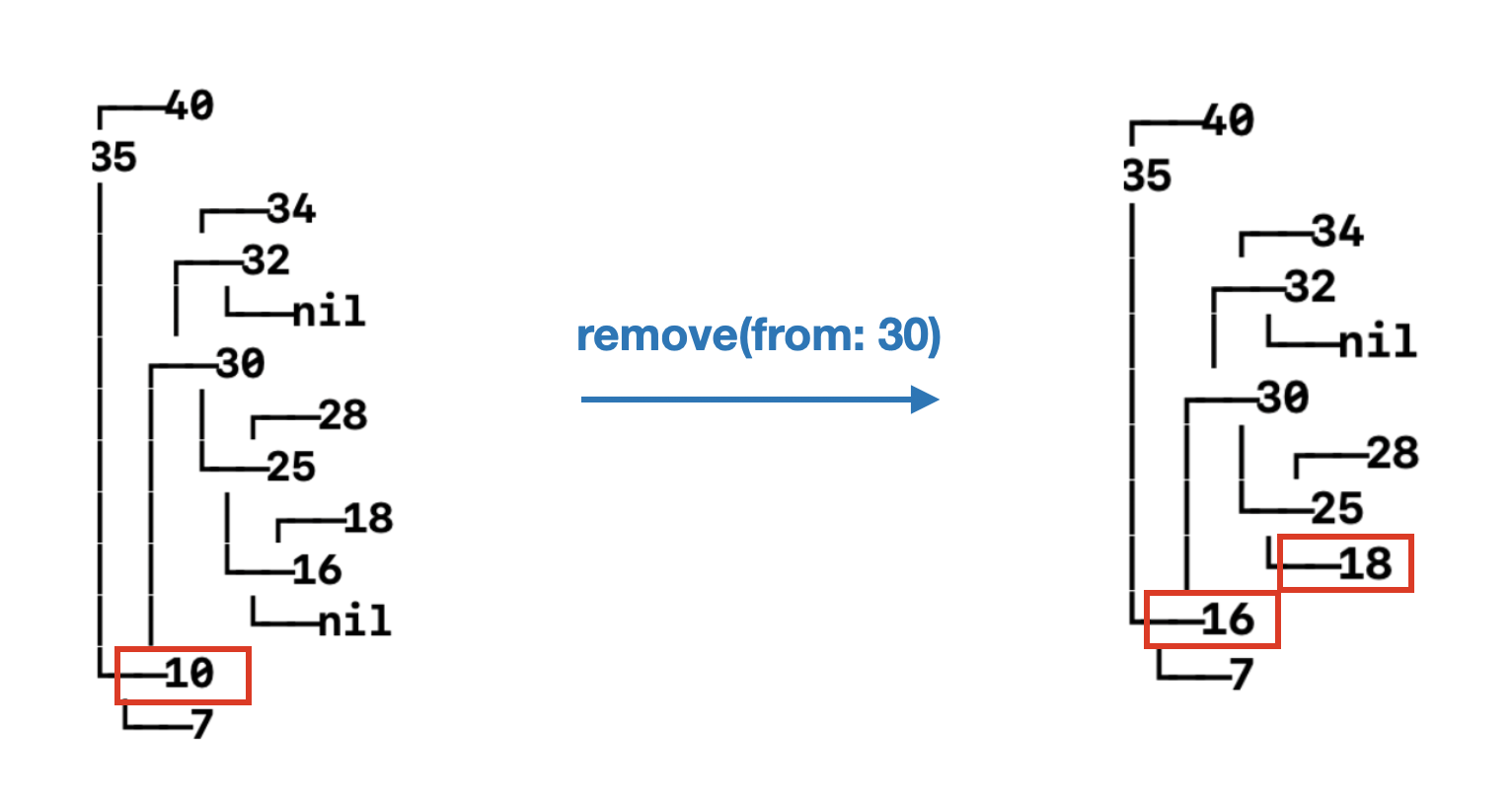
10이 삭제도 잘 됐고! 우리가 원하는 모양으로 트리도 잘 바뀌었음 :)
Delete Node(10)의 자리에 오른쪽 자식 노드(30) 중 가장 작은 값인 Change Node(16)이 들어갔고,
Change Node의 자식 노드 18은 Change Parent Node의 왼쪽으로 붙었음!
꺄아아악 힘들다
보통 위 두 가지 방법 중 하나로 하면 되는데,
2번째 방법 코드가 궁금해여ㅠㅠ!! 하면 말해주셈 추가하겠셈 (지금은 귀찮아 힘들어)
remove의 전체 코드 보고 싶으면 더보기 눌러주셈
|
func remove(from data: T) -> Bool {
guard let root = self.root, root.data != data else { return false }
var parentNode = root
var currentNode: Node? = root
//삭제할 노드 탐색
while let node = currentNode {
if node.data == data {
break
}
if node.data > data {
currentNode = node.left
} else {
currentNode = node.right
}
parentNode = node
}
guardet deleteNode = currentNode else { //탐색 실패
return false
}
// 1. 자식이 없는 노드 삭제(Leaf Node)
if deleteNode.left == nil && deleteNode.right == nil {
if parentNode.data > data {
parentNode.left = nil
} else {
parentNode.right = nil
}
return true
}
// 2. 자식이 1개 있는 노드 삭제
if (deleteNode.left != nil) && (deleteNode.right == nil) {
if parentNode.data > data {
parentNode.left = deleteNode.left
} else {
parentNode.right = deleteNode.left
}
return true
}
if (deleteNode.left == nil) && (deleteNode.right != nil) {
if parentNode.data > data {
parentNode.left = deleteNode.right
} else {
parentNode.right = deleteNode.right
}
return true
}
// 3. 자식이 2개 있는 노드 삭제
guard let rightNode = deleteNode.right else { return false }
var changeNode = rightNode
var changeParentNode = rightNode
while let nextNode = changeNode.left {
changeParentNode = changeNode
changeNode = nextNode
}
if let rightNode = changeNode.right {
changeParentNode.left = rightNode
} else {
changeParentNode.left = nil
}
if parentNode.data > data {
parentNode.left = changeNode
} else {
parentNode.right = changeNode
}
// Delete Node의 왼쪽, 오른쪽 자식을 changeNode에게 이식
changeNode.left = deleteNode.left
changeNode.right = deleteNode.right
return true
}
|
BST의 전체 코드는 마지막에 내 깃허브 주소로 추가해 놓겠셈!
4. 이진 탐색트리의 사용 용도 및 장점 / 단점
자, 먼저 이진탐색은 그럼 언제, 왜 쓸까??
이름에 떡하니 써있음 이진 "탐색" 트리... ㅎ 말 그대로
데이터를 탐색
할 때 씀....! 왜냐? 탐색 속도가 엄청 빠르거든
탐색 속도가 어떻게 빠른지 배열과 비교하는 다음 짤을 보셈
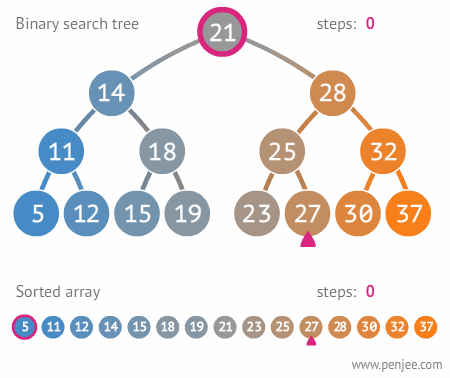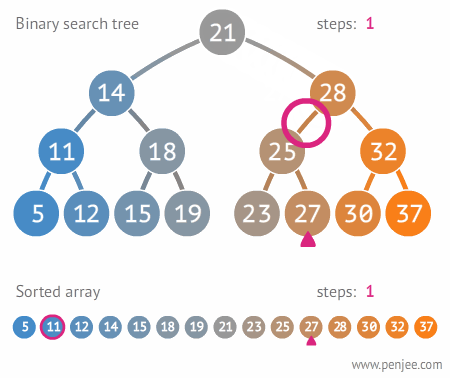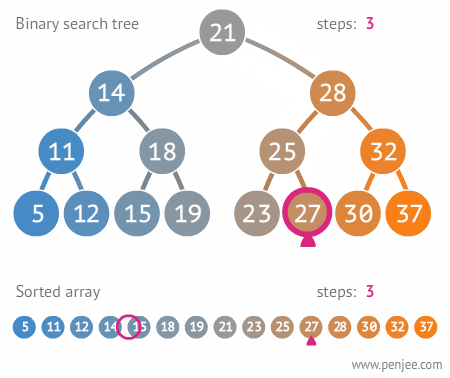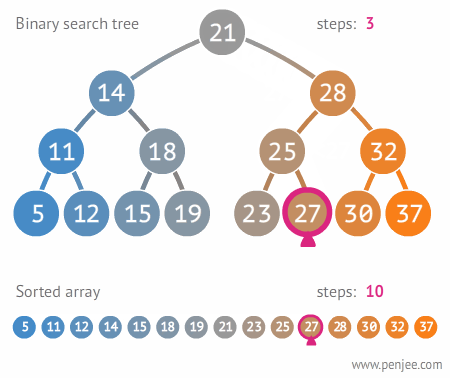
이거 보세요
배열이 11번 탐색할 동안, 이진 탐색 트리는 3번만 탐색하면 된다는 것이요
허허 고놈 참 쓸모있구먼
그렇지만, 단점도 있는데
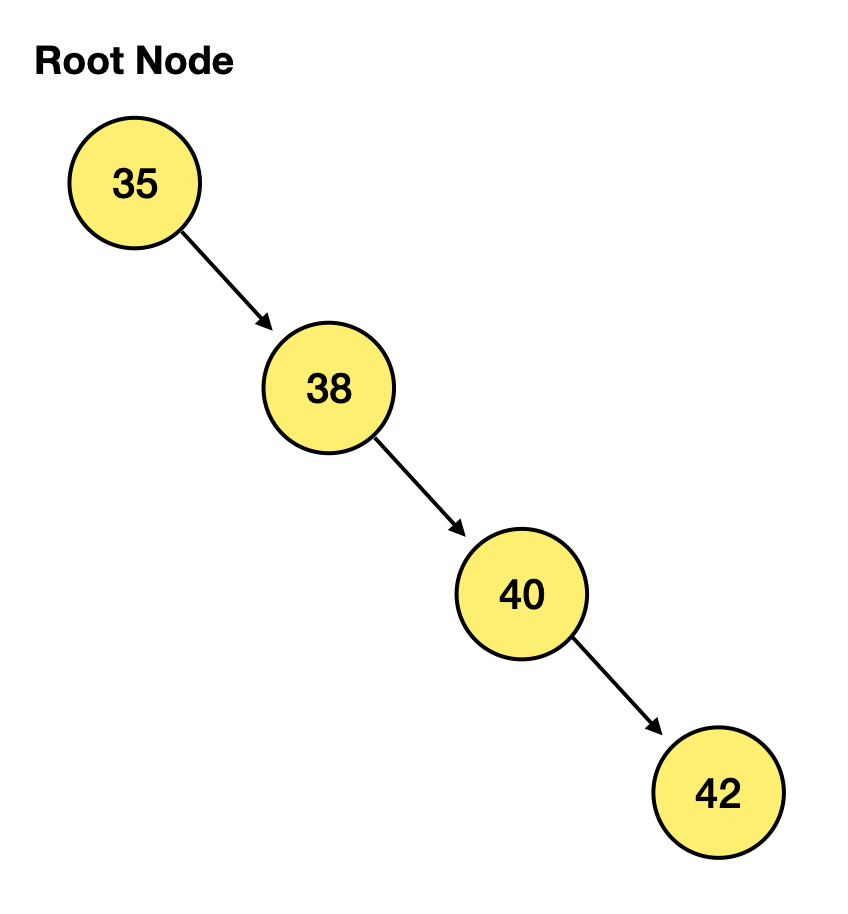
이렇게 못배워먹은 듯 생긴 이진탐색트리는
배열과 탐색 시간이 별 다를바가 없다~~~~~~
바로 다음에 배우겠지만 시간 복잡도가 O(n)으로 배열과 동일하다~~
근데 간혹가다 생기는 이런 경우 빼곤, 일반 배열보다 탐색이 훨~ 씬 빠름!
얼마나 빠른지 시간 복잡도로 봐보자 :)
5. 이진탐색트리(BST)의 시간 복잡도
자!!! 마지막 시간~~
이진탐색트리의 시간 복잡도에 대해서 알아볼 것임 :)
길게 말하지 않겠음...
n개의 노드를 가질 때, 이진 탐색 트리의 시간 복잡도는
O(𝑙𝑜𝑔𝑛)
녀러분 빅오표기법에서 𝑙𝑜𝑔𝑛의 밑은 10이 아니라 2랍니닫....
근데 뭐라고??
못배워먹은 이진탐색트리는 O(n)으로 배열과 동일할 수도 있다~~
.
.
.
그럼 끗!
근데 내가 공부하고 적용한 건 여기까진데...
루트노드는 삭제 못하나......? 라는 의문이 ;ㅁ;.. 찾아봐도 없음 ㅜㅜ내가 못찾은 건지
개인 코드에선 루트노드는 삭제 못하게 막아두긴 했는데.. 뭐 나중에 알게되면 추가하겠음
그럼 20,000~
피드백 혹은 궁금한점은 언제든 댓글 달아주세요 😇
전체 코드는 제 깃허브에서 봐주시고, 출처는 1편에서 모두 표기 했습니다 :)
'Algorithm > 자료구조' 카테고리의 다른 글
| Swift) 그래프(Graph) 이해하기 (6) | 2021.01.20 |
|---|---|
| Swift) 이진 탐색 트리(BST) 구현 해보기 (1/2) (5) | 2021.01.06 |
| Swift) 해시 테이블(Hash Table) 이해하기 (13) | 2021.01.05 |
| Swift) 양방향 연결 리스트(Doubly LinkedList) 구현 해보기 (5) | 2021.01.04 |
| Swift) 단방향 연결 리스트(LinkedList) 구현 해보기 (6) | 2020.12.29 |



