안녕하세요, 소들입니다 :)
오늘은 저번 포스팅에 이어, 최소 신장 트리 중 프림 알고리즘에 대해 포스팅을 해볼 건데요..
만약 최소 신장 트리가 뭐야? 크루스칼 알고리즘이 뭐야? 하시는 분은 이 포스팅을 먼저 읽고 오시길 ...!!! 👀
참고로 크루스칼보다 훨~~~~~~~~~ 쉬우니 맘 편하게 봅시다!!!!!!!
그럼 알아보러 갑시다 :)
모든 포스팅은 편의 말투로 합니다~!!
1. 프림 알고리즘의 로직
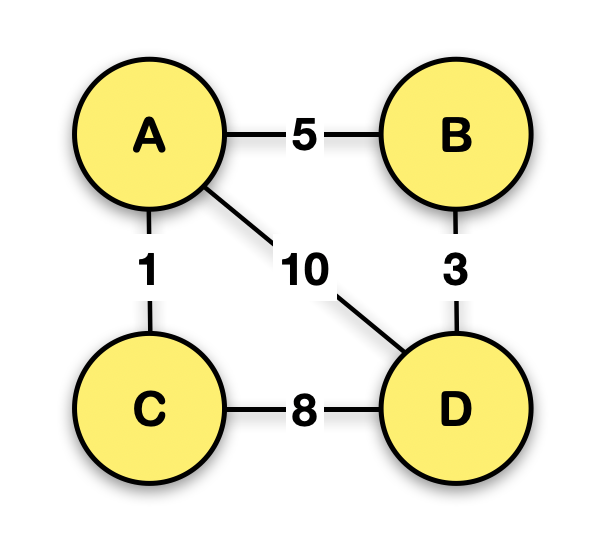
크루스칼과 마찬가지로 위 그래프를 갖고
프림 알고리즘을 통해 최소 신장 트리를 찾는 방법을 알아 보겠음!!!!
1-1. 시작 노드(A)를 정하고, 이를 "연결된 노드 집합"에 삽입한다
가장 작은 간선의 가중치부터 시작하는 크루스칼과 달리, 프림은 시작 노드를 임의로 정함!
내가 만약 시작 노드를 A로 정했다면,
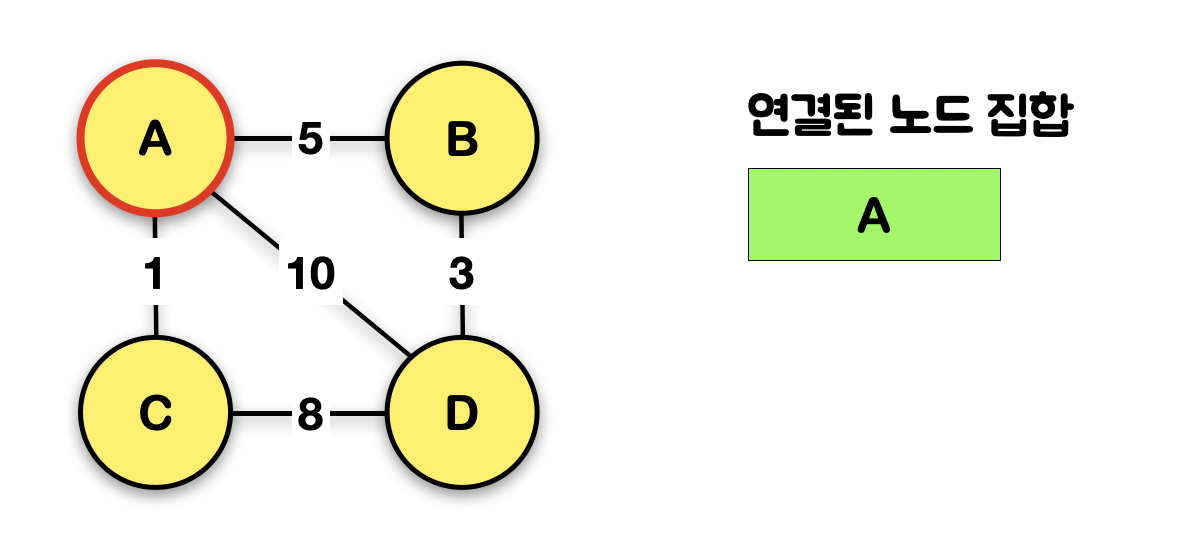
이렇게 A를 연결된 노드 집합이란 자료형에 삽입함!!!!
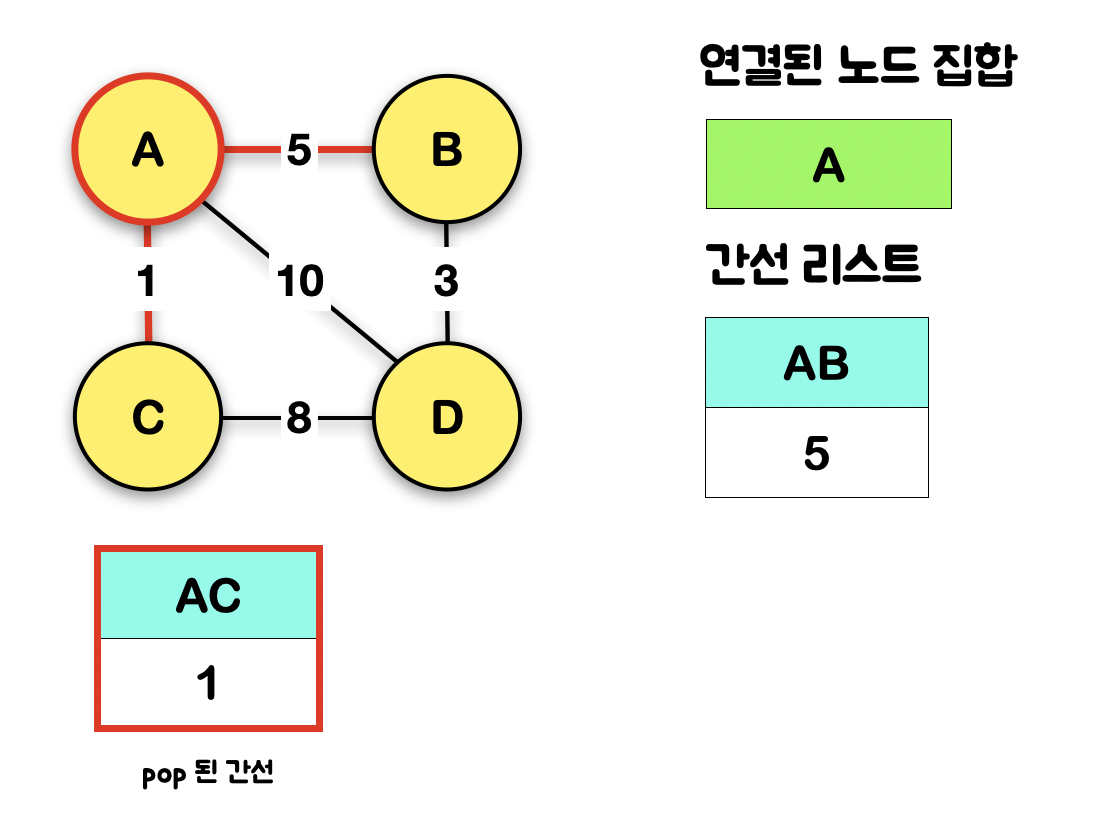
1-2. A와 연결된 간선들을 "간선 리스트"에 삽입한다

간선 리스트란 자료형 또한 필요 하겠군 ㅎ.ㅎ...!
1-3. 간선 리스트에 저장된 간선 중, 가장 가중치가 작은 간선을 꺼낸다(pop)
1-4. 만약 해당 간선(AC)의 도착지(C)가 "연결된 노드 집합"에 있다면 사이클이 발생한단 것으로 스킵하기 때문에 "간선 리스트"에서 다시 가장 작은 간선을 꺼내오고, 만약 도착지(C)가 "연결된 노드 집합"에 없다면 해당 간선(AC)을 "선택 리스트"에 넣고, 도착지(C)도 "연결된 노드 집합"에 넣고, 도착지(C)와 연결된 간선을 "간선 리스트"에 삽입한다
길다고 겁먹지 마셈... 한글자씩 읽으며ㅕㄴ 매우 단순함..
AC 간선의 경우, 도착지인 C가 "연결된 노드 집합"에 포함되어 있지 않기 때문에
스킵하고 간선을 다시 꺼내올 필요 없이,
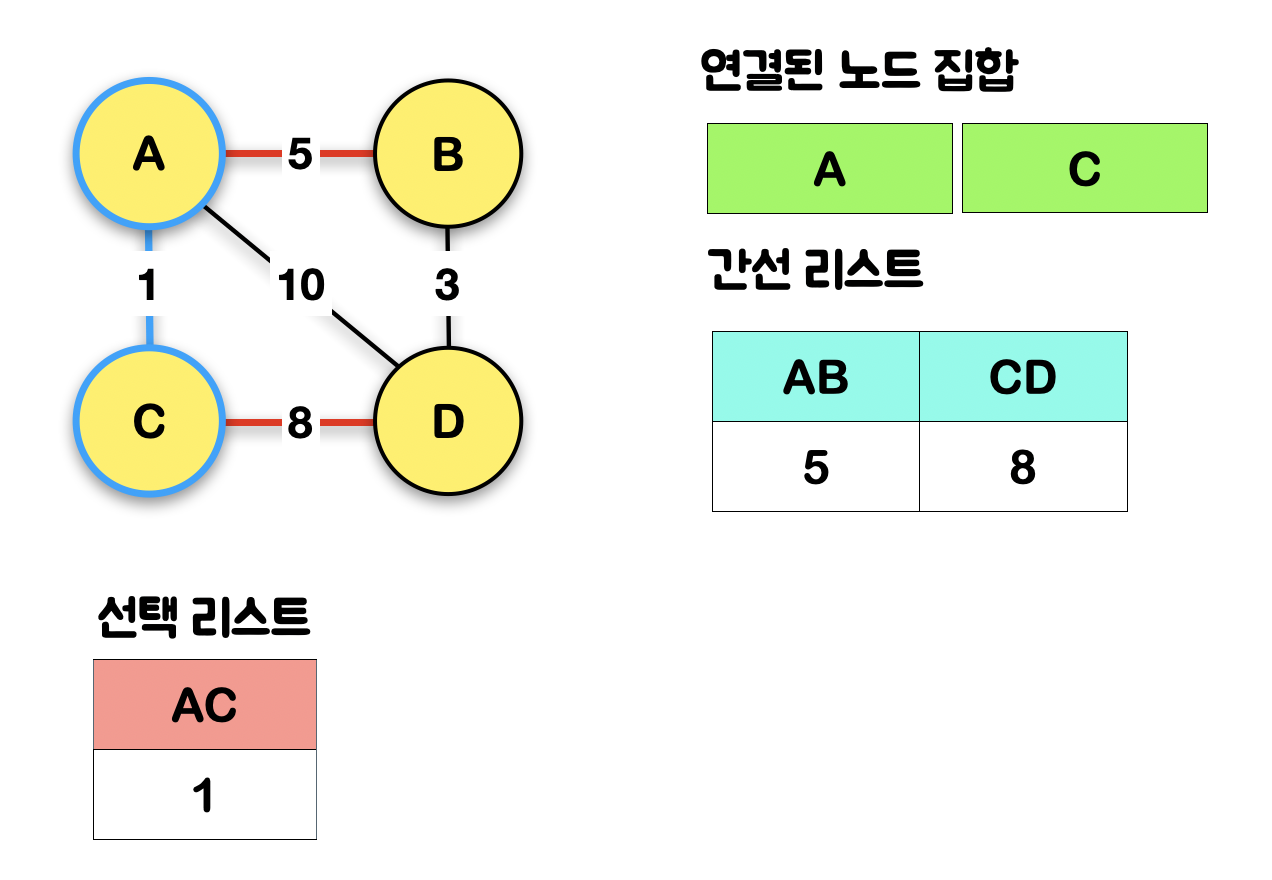
AC를 "선택 리스트"에 넣고, 도착지 C도 "연결된 노드 집합"에 넣고,
C와 연결된 간선을 모두 간선 리스트에 삽입해줬음!!
이제 이 과정을 연결된 노드의 집합 갯수가, 노드의 갯수가 될 때까지 반복하는 것임!!
모든 노드를 한번씩 다 들렸다는 것이기 때문! 계속해서 그림으로 보여주겠음!
1-5. 간선 리스트에 저장된 간선 중, 가장 가중치가 작은 간선을 꺼낸다(pop)
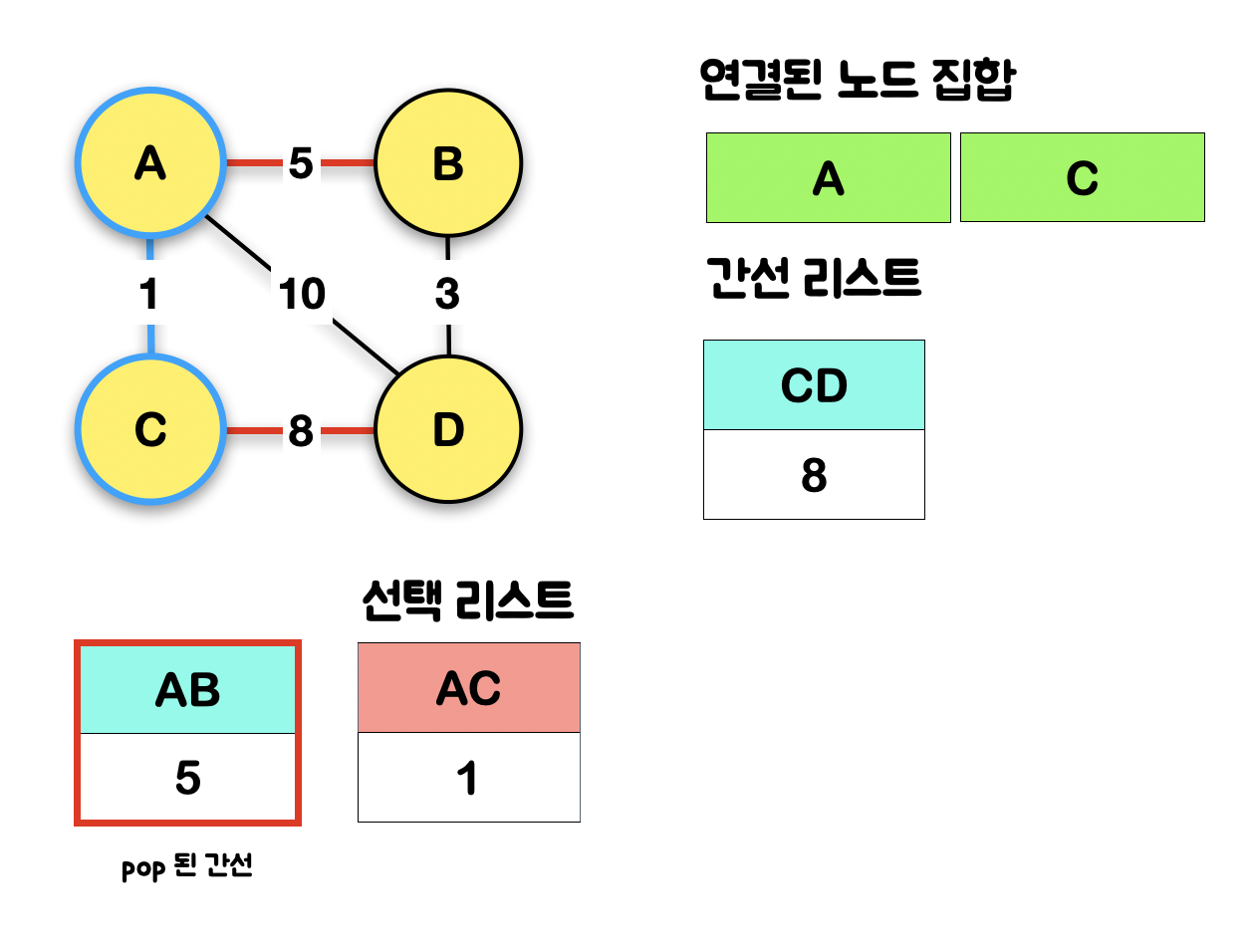
1-6. 만약 해당 간선(AB)의 도착지(B)가 "연결된 노드 집합"에 있다면 사이클이 발생한단 것으로 스킵하기 때문에 "간선 리스트"에서 다시 가장 작은 간선을 꺼내오고, 만약 도착지(B)가 "연결된 노드 집합"에 없다면 해당 간선(AB)을 "선택 리스트"에 넣고, 도착지(B)도 "연결된 노드 집합"에 넣고, 도착지(B)와 연결된 간선을 "간선 리스트"에 삽입한다
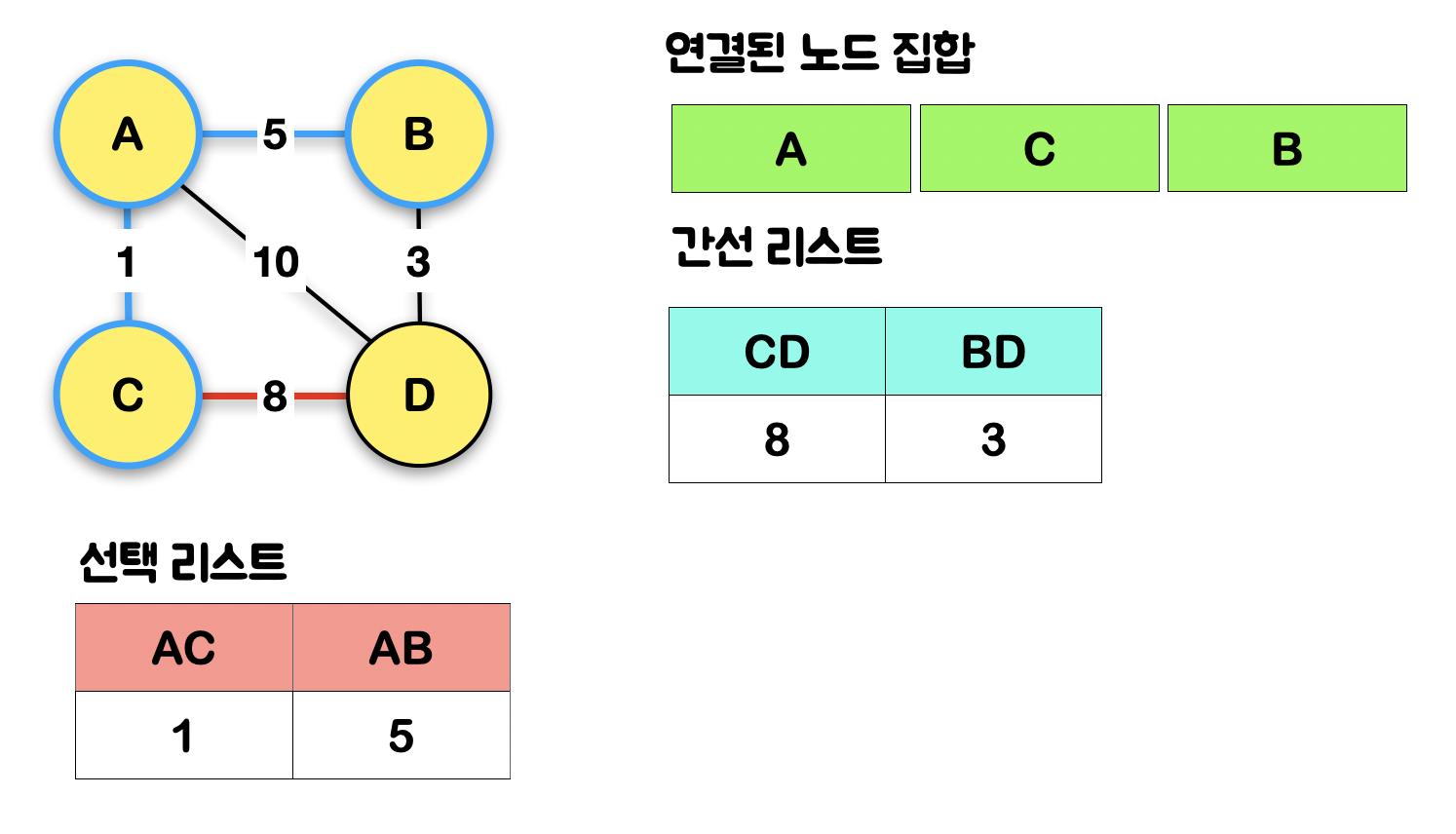
1-7. 간선 리스트에 저장된 간선 중, 가장 가중치가 작은 간선을 꺼낸다(pop)

1-8. 만약 해당 간선(BD)의 도착지(D)가 "연결된 노드 집합"에 있다면 사이클이 발생한단 것으로 스킵하기 때문에 "간선 리스트"에서 다시 가장 작은 간선을 꺼내오고, 만약 도착지(D)가 "연결된 노드 집합"에 없다면 해당 간선(BD)을 "선택 리스트"에 넣고, 도착지(D)도 "연결된 노드 집합"에 넣고, 도착지(D)와 연결된 간선을 "간선 리스트"에 삽입한다

이렇게!! 연결된 노드 집합의 갯수(4) == 노드의 갯수(4) 가 되는 순간!!
더이상 반복하지 않고 끝내면 됨!!!!!!!
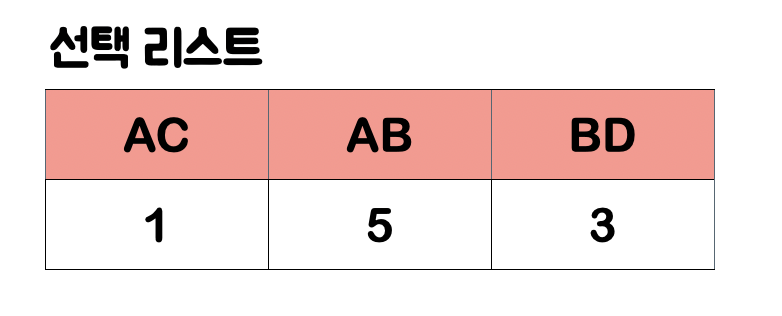
이 선택 리스트에 있는 이것들이 바로, 프림 알고리즘으로 얻은 최소 신장 트리의 간선이 되는 것임 :)
이를 이제 코드로 구현 해보자!!
2. 코드로 구현 해보기
4-1. 탐색할 그래프 미리 만들어두기
음.. ~ 여기선 데이터를 갖고 그래프를 어떻게 구현하냐!는 다루지 않음
다만, 이미 구현되어 있는 그래프를 어떻게 탐색하는지만 다룰 것임 :)
|
struct Edge: Comparable {
var start: String = ""
var dest: String = ""
var weight: Int = 0
init(_ start: String, _ dest: String, weight: Int) {
self.start = start
self.dest = dest
self.weight = weight
}
static func < (lhs: Edge, rhs: Edge) -> Bool {
lhs.weight < rhs.weight
}
}
let vertices = ["A", "B", "C", "D"]
let edges: [Edge] = [
.init("A", "B", weight: 5),
.init("A", "C", weight: 1),
.init("A", "D", weight: 10),
.init("B", "A", weight: 5),
.init("B", "D", weight: 3),
.init("C", "A", weight: 1),
.init("C", "D", weight: 8),
.init("D", "A", weight: 10),
.init("D", "B", weight: 3),
.init("D", "C", weight: 8)
]
|
하드코딩 완료.....ㅎ
verices는 각각 노드를 담은 거고, enges는 간선들의 정보를 담은 것임!
왜 struct를 따로 만들었냐면 ㅠㅠㅠㅠ Swift에서 내가 구현한 Heap은 Comparable 프로토콜을
채택하고 있기 때문에..! 간선을 힙에 넣고, 가중치에 따라 우선 순위를 주기 위해서 한 것임!!!
2-2. 간선의 최소 값을 pop할 우선 순위 큐를 구현하자
Swift는 힙을 자체적으로 제공하지 않기 때문에 ㅠ.ㅠ(파이썬은 제공함)
이는 이전에 구현했던 내 힙 코드를 그대로 쓰겠음..! 요기 가면 전체 코드 볼 수 있음!!
2-3. prim 함수 구현하기
|
typealias edge = (Int, String, String)
func prim(start: String, vertices: [String], edges: [Edge]) -> [edge]? {
var mst: [edge] = [] // 선택 리스트
var edgeList = MinHeap<Edge>() // 간선 리스트
var connectedNode: Set<String> = [] // 연결된 노드 집합
var adjacentEdges: [String: [Edge]] = [:] // 모든 노드에 연결된 모든 간선을 저장하는 딕셔너리
for vertice in vertices {
adjacentEdges.updateValue([], forKey: vertice)
}
for edge in edges {
adjacentEdges[edge.start]?.append(edge)
}
guard let startEdges = adjacentEdges[start] else { return nil }
connectedNode.insert(start) // 처음 선택된 노드를 선택 리스트에 삽입
for edge in startEdges { // 처음 선택된 노드에 대한 간선들을 간선 리스트에 삽입
edgeList.insert(edge)
}
while mst.count < vertices.count {
guard let poppedEdge = edgeList.pop() else { break }
if connectedNode.contains(poppedEdge.dest) { continue }
mst.append((poppedEdge.weight, poppedEdge.start, poppedEdge.dest))
connectedNode.insert(poppedEdge.dest)
guard let destEdges = adjacentEdges[poppedEdge.dest] else { return nil }
for edge in destEdges {
if !connectedNode.contains(edge.dest) {
edgeList.insert(edge)
}
}
}
return mst
}
|
ㅎㅎ...;;;
이렇게 짜면 잘은 굴러 가는데...............
일단 코드가 너무너무너무너무 너무너무맘에 안들음..;;;;;;
공부하자마자 뜨끈뜨끈하게 참고하면서 Swift로짜보는 거라 그런지
너무 지저분한 코드도 많고ㅠㅠㅠㅠㅠ 에휴.. 나중에 더 예쁜 코드가 생각나면 수정 할게요 ㅠ.ㅠ
(코드 피드백 대 환 영...)
3. 프림 알고리즘 시간 복잡도
최악의 경우 모든 간선에 대해 반복하고, 최소 힙을 사용하므로..!!!
O(𝐸𝑙𝑜𝑔𝐸)
의 시간 복잡도를 가짐 XD
4. 개선된 프림 알고리즘
사실 프림 알고리즘은 최악의 경우 모든 간선을 반복해야 해서..
우선 순위를 간선에 두지 말고 노드에 두자!!!!!! 해서 나온 시간 복잡도를 줄이는 개선된 프림 알고리즘이 있는데..
이걸 공부하고 스위프트로 구현 해볼라 했는데......
개선된 프림 알고리즘은 Heap에서 Update란 기능을 쓴단 말임??
근데 Swift는 힙을 제공하지도 않을 뿐더러, 내가 만든 힙은 Update란 기능이 없어서..
(추가하기에 넘 복잡함;;)
따라서 개선된 프림 알고리즘은 따로 포스팅하지 않게씀...........
파이썬 하시는 분들은 파이썬으로 공부하시길............ /_\ 소무룩..
.
.
.
흠...................... 이로써 최소 신장 트리 알고리즘은 모두 끝인데......
코드가 넘 맘에 안들어서 ㅠ.ㅠ... 계속 다시 보고 공부하며,
더 나은 코드가 생각나면 추가 하겠습니다ㅏ...ㅠ.ㅠ.........
피그백 & 궁금증은 언제나 댓글 남겨 주세요 :)
'Algorithm > 알고리즘' 카테고리의 다른 글
| Swift) 최소 신장 트리 :: 크루스칼 알고리즘(Kruskal’s algorithm) 구현 해보기 (0) | 2021.02.02 |
|---|---|
| Swift) 최단 경로 :: 다익스트라(Dijkstra) 구현 해보기 (5) | 2021.01.27 |
| Swift) 힙(Heap) 구현 해보기 (8) | 2021.01.27 |
| Swift) 탐욕법 (Greedy Algorithm) + 프로그래머스 체육복 풀이 (4) | 2021.01.25 |
| Swift) 깊이 우선 탐색(DFS) 구현 해보기 (10) | 2021.01.20 |



